Cai等人最早提出一种GNMF方法,其通过构建最近邻图来编码原始数据中的几何信息,并在构建的图邻接矩阵上实现非负矩阵分解。GNMF模型的目标函数表示如下:


大量的GNMF算法均利用了流形结构这一先验知识建立样本之间的图邻接矩阵,其首先利用距离度量确立两个样本之间的连接关系,如K近邻图,ε邻域图等,然后根据热核函数或者欧式距离函数确立两个样本之间的连接权重wij。热核函数和欧式距离函数的表达形式如公式(4-42)和公式(4-43)。

式中,t表示热核参数,NN(xi)表示xi的K近邻或ε邻域。但是,这些图邻接矩阵的构造方法都是基于最近邻关系和欧式距离函数,对参数的选择具有比较大的依赖性,使得构造的邻接矩阵不具备稀疏性和对噪声的鲁棒性,也导致构造的图邻接矩阵不能体现样本之间的类别关系。
为了解决传统基于欧式距离的图邻接矩阵构造缺陷,Cheng等人率先将稀疏表示理论引入到图构建过程,提出一种稀疏图构造方法。这类方法将每一个样本看成是剩余所有样本的稀疏表示,即每个样本都是其他所有样本的线性组合,得到该样本的稀疏表示系数,然后根据稀疏表示系数确定两个顶点之间的权重,最后基于构建的稀疏图进行各种算法的学习。利用稀疏表示模型进行图邻接矩阵的构建,不仅省去了大量的欧式距离计算,还能够得到更加稀疏的图结构。
接下来,简单介绍如何利用稀疏表示模型进行图邻接矩阵的建立。对于一个给定的样本集X=[x1,x2,…,xn],稀疏图有如下的构建过程。
(1)首先求解每个xi关于Xi=[x1,…,xi-1,xi+1,…,xn],i=1,…,n的稀疏表示:(https://www.xing528.com)
![]()
式中,αi=[αi1,…,αij,…,αn]T,i=1,..n,j≠i表示xi的稀疏表示系数,‖·‖1表示向量的1范数,即非零元素的绝对值之和。
(2)然后根据步骤(1)中的稀疏表示系数绝对值计算稀疏图的权重。将构造的稀疏图记为G=(V,E),则图中两个顶点的连接权重wij计算方式为公式(4-45)。

公式(4-44)中的优化问题是一个典型的凸优化问题,该问题存在唯一的全局最优解,可通过Least Absolute Shrinkage and Selection Operator(LASSO)算法进行求解。对于5个行为类别以及50个样本的IDT-HOG-HOF-MBH特征,图4-18展示了由公式(4-44)和公式(4-45)得到的稀疏图与传统的K近邻图以及ε邻域图的邻接矩阵对比。从图中可以看出用稀疏表示方法得到的图邻接矩阵具有更加稀疏的结构,也更能表示同类别样本数据之间的关系,即每10个样本之间有更多的连接权重。但是,由于没有考虑到样本之间距离关系,使得稀疏图中存在一些不相关的连接关系,即图4-18(c)中的离散区域。因此,本节使用样本的相似关系来约束公式(4-44)中的目标函数,从而得到更能描述样本语义关系的稀疏图结构。
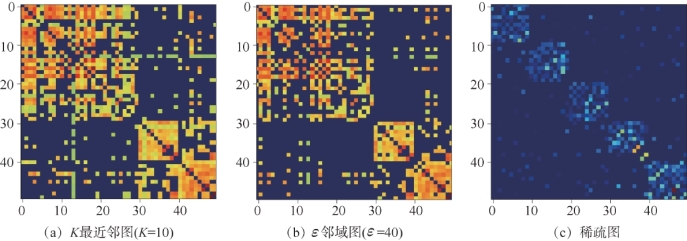
图4-18 可视化的图邻接矩阵
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




