谱回归判别分析算法在深度网络人脸识别中的应用

本节介绍谱回归判别分析深度网络（Spectral Regression Discriminant Analysis Network，SRDANet）人脸识别算法，解决现有CNN模型在网络参数的学习过程中需要大量标注样本的问题，减小了现有CNN模型的训练成本，扩展了CNN模型的适用范围。而且，SRDANet算法通过一次前向传播即可确定整个模型的参数，从而避免了CNN模型由于BP算法的迭代优化而导致的训练时间过长问题。

SRDANet模型主要由卷积层、非线性处理层、池化层和输出层这四部分组成。在SRDANet模型的卷积层中，利用有监督的SRDA算法提取人脸图像块（facial patches）中的主要特征向量（leading eigenvectors），然后将其变形（reshape）为矩阵的形式并作为卷积层的卷积核。为了配合SRDANet模型特殊的卷积核学习方式，SRDANet模型的非线性处理层只出现于所有卷积层之后，并使用简单的二值哈希作为激活函数。在池化层中，经过非线性处理层后的特征图转化为了一系列二值图像，参考LBP算法的编码（encoding）策略，为每个特征图赋以权重。然后对特征图按元素相加，最终得到一幅实数值特征图。最后，通过直方图的形式统计该实数值图像上每个值的出现频率，并将其作为最终的输出特征。以两阶段的SRDANet模型为例，图2-20展示了SRDANet模型的结构框图。

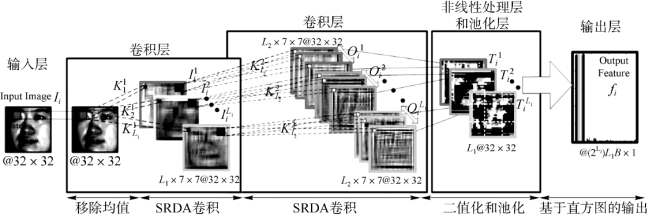
图2-20　基于两层的SRDANet模型结构框图

1.SRDANet的卷积层

假设训练集提供了一系列属于c个类别的N个训练样本{Ii}Ni=1每幅人脸图像的大小为d1×d2（d1×d2=d）。由于卷积运算可以提取通过卷积核提取得到局部纹理模式或全局结构信息，因此在本算法中沿用CNN模型中的卷积运算。SRDANet模型在所有卷积层中的卷积核尺寸均为j1×j2，第i个卷积层中有Li个卷积核。不同的是，SRDANet模型采用子空间学习算法确定深度模型的卷积核参数，而不是通过反向传播算法迭代优化得到。

对于第i幅人脸图像而言，在每个像素点采样大小为j1×j2的局部图像块，采样步长为s，从而得到了M个大小为j1×j2的局部图像块集合Pi=[pi，1，pi，2，…，pi，M]。为了使学习得到的卷积核能够更有效地描述原始数据的变化情况，对集合Pi进行去均值。对所有训练样本（个数为N）重复上述的局部块提取操作，可以得到：

接下来，从矩阵P中利用谱回归判别分析算法学习第i层特征图的主要的特征向量V（i）。谱回归判别分析旨在学习投影方向（即特征向量）使同类数据点之间尽可能接近，而不同类数据点之间则尽可能远离。其目标函数如下所示：

式中，Sb表示类间散布矩阵（between-class scatter matrix），而St表示整体散布矩阵（total scatter matrix）。为了更清晰地表达SRDANet算法卷积层的运算，矩阵X通过谱回归判别分析算法得到前l2个特征向量的运算可以被简化为SRl1（X）。

接下来，将学习得到的一系列一维特征向量变形为一系列二维矩阵，并将这些二维矩阵作为SRDANet算法的卷积核。将这些特征向量变形为矩阵并将其作为卷积核，可以提取人脸图像中具有判别力的局部模式。所以，SRDANet模型通过一次前向传播即可学习得到所有卷积层中的参数（即卷积核）。SRDANet模型从原始图像块集合P中学习得到的卷积核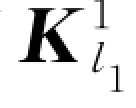，其数学表达形式如下：

式中，vec2matj1，j2（·）表示将长度为j1j2的一维向量变形为大小为j1×j2的二维矩阵，而c则表示类别数。因此，SRDANet模型第一层的输出（特征图）可以表示为

式中，*表示二维卷积运算。将Ii的边缘填充0元素，从而使I l 1i与Ii具有相同的尺寸。(www.xing528.com)

谱回归判别分析可以得到（c-1）个非零特征向量，因此，SRDANet在第一层共有（c-1）特征图。而SRDANet模型中的第二层会对第一层的每个特征图再分别提取（c-1）特征图，因此，SRDANet模型中的第二层会输出（c-1）2个特征图。一方面，小特征值对应的特征向量描述的是某个人脸图像中包含的特殊信息，而非所有人脸图像中包含的共有信息。因此，用这种特征向量作为卷积核，难以从人脸图像中提取得到具有判别能力的信息；另一方面，当训练样本的类别数c比较大时，SRDANet算法会随着网络层数的不断加深，消耗更多的运算资源。因此，只取特征向量中前L1个特征向量作为卷积核，即

式中，l1=1，2，…，L1，i=1，2，…，N。

2.SRDANet的非线性处理层

SRDANet算法中卷积核的本质可以理解为利用SRDA算法学习得到的特征向量，特征值越大的特征向量对应着判别能力越强的卷积核。相比于最后一个卷积核，第一个卷积核的重要程度会高很多。因此，第一个卷积核对应的二值输出会被赋予更大的权重。将一系列二值图像按照LBP算法中权重求和的策略，转化为一个实数值图像，上述过程可以表示为如下的数学公式：

式中，图像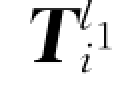中像素点的取值范围为[0，2L 2-1]。经过加权求和的运算，一系列二值的特征图被转化为了一个实数值特征图，而针对特征图的池化运算也将在实数值的特征图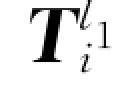上进行。

3.SRDANet的特征池化层

4.SRDANet的计算复杂度

以两层的SRDANet模型为例，并采用每秒浮点运算次数（FLoating-point Operations Per Second，FLOPS）作为评价SRDANet计算复杂度的指标。在卷积层中，对于每个卷积层构建去均值后的数据矩阵P均需要（j1j2+j1j2 d1 d2）FLOPS；而从训练样本集中学习SRDA卷积核则需要[Nd1 d2（j1j2）2+O（Nd1 d2j1j2）]FLOPS；对于每个卷积层中，图像与SRDA卷积核卷积运算均需要L1 d1 d2j1j2 FLOPS；在非线性处理层中，将L2个二值图像转化为一个实数值图像则需要2L2 d1 d2j1j2；在池化层中，提取并连接基于图像块的直方图特征的计算复杂度为O（d1d2BL2 log2）。由于d≫max（j1，j2，L1，L2，B），因此SRDANet模型的计算复杂度可以近似为