迭代量化二值编码人脸识别算法

本节介绍基于迭代量化的二值编码（Iterative Quantization Binary Codes，IQBC）人脸识别算法，旨在提升现有二值特征人脸识别算法在非约束环境下的描述能力。二值特征只能采用-1或1两个元素对特征进行表示，相比同等输出维度的实数值特征，二值特征虽然具有较为优秀的鲁棒性，但其携带信息的能力（即特征的描述能力）要远弱于基于实数值的特征。

为了在保证二值特征鲁棒性的基础上，提升二值特征的描述能力，IQBC算法创新性地从量化误差、特征表达和正交约束三个角度对目标函数进行考虑，提升二值特征的描述能力。在量化误差项中，IQBC算法通过结合多类谱聚类（multi-class spectral clustering）和正交普氏分析（orthogonal Procrustes problem）现有理论，学习得到一种优化的投影方式，将去均值后的数据旋转至线性可分的二值表示空间，保证了实数值特征与二值特征之间的量化误差最小。在特征表达项中，IQBC算法要求在每个比特上都具有最大的方差，从而提升了特征携带信息的能力，即算法的描述能力。在约束项中，IQBC算法要求在二值特征的每个比特之间应该相互独立。正交约束使得特征在相同维度的情况下，能够携带更多的信息。

IQBC人脸识别算法的算法流程如图2-13所示。首先，提取基于实数值的像素差值向量；然后利用基于迭代量化的二值编码算法将像素差值向量量化为二值特征；最后，利用聚类和池化的方法，对二值特征进行基于词典模型形式的表达。本节仅介绍IQBC算法的核心部分——基于迭代量化的二值编码过程。

1.目标函数的建立

接下来，对三个优化项的数学形式和物理含义进行详细介绍。

（1）约束项：当比特之间相互独立（即正交）时，即B T B=n I，二值特征能够携带最多的信息，从而拥有最优秀的描述能力。但由于符号函数sgn（·）的存在，使得针对二值特征的正交约束难以求解。因此，针对二值特征的正交约束则可以转化为针对投影矩阵的约束，即W T W=I。

（2）特征表达项：为了让学习得到的特征在一定长度下能够携带最多的信息，从而提升其描述能力，IQBC算法还要求每个比特的方差最大化，即

上述的目标函数（2-22）与PCA算法的目标函数一致。因此，使长度为L的二值特征中每个比特方差最大的目标，等价于从PDVs的协方差矩阵中提取前L个最大特征值对应的特征向量。当算法提取得到像素差值向量X后，首先对其进行PCA运算，得到由特征向量组成的投影矩阵W=[w1，w2，…，wL]。

（3）量化误差项：假设W∈R d×L为PCA算法的投影矩阵，其中每一列表示一个特征向量。则V=XW∈R NM×L表示经过PCA投影后的数据矩阵。直接投影后的特征矩阵V并不具有很强的判别能力，如果直接对V进行硬二值化运算，会使得同一个人的实数值特征编码为不同的二值向量，如图2-15（a）所示。因此，需要对V进行空间旋转，使得同一个人的二值特征位于相同的象限，如图2-15（c）所示。由于矩阵W为公式（2-22）的最优解，所以任何同维度的正交矩阵R∈R L×L也都是公式（2-22）的最优解。因此，经过旋转后的量化误差

式中，W为PCA的投影矩阵，而R为二值量化的旋转投影矩阵。综上所述，IQBC算法中共有三个优化项——量化误差项、特征表示项和约束项。其中，量化误差项减少了从实数值特征到二值特征的信息损失。特征表示使得IQBC特征在每位比特上都能携带最多的信息量，从而提升了算法的描述能力。而约束项采用的是正交约束，该约束使得IQBC特征在相同维度的情况下，能够携带更多的信息，同样提升了算法的描述能力。

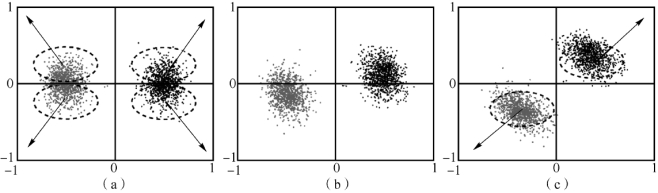
图2-15　硬二值化过程就是将每个像素点量化为与其距离最近的顶点，即（±1，±1）(www.xing528.com)

图（a）中x轴和y轴对应着原始数据的PCA投影方向。未经过旋转的数据会将同一个人分配到不同的顶点，即不同的二值编码上去；（b）一次随机旋转则会使错误分配的误差降低；（c）通过迭代量化学习到的最优化的旋转则会使得投影后的聚类结构与原始数据的标签近乎一致，并使得分配误差降到最低

2.目标函数的优化

IQBC的目标函数（即公式（2-23））在B和R同时变化时是非凸的，只有当B和R其中一个变量固定时，该目标函数才是凸的。因此，利用迭代优化的思想，在固定其中一个变量的同时更新另一个变量。

固定R更新B：当R固定时，公式（2-23）可以展开成如下形式：

式中，Uij表示旋转后的矩阵U=VR中的对应元素。显然地，当Uij和Bij具有相同符号时，tr（BR T V T）可获得最大值。因此，当R固定时，B的解可以表示为

固定B更新R：当B固定时，公式（2-23）即退化为最小二乘问题（least-squares problem），当R又有正交约束时，最小二乘问题则进一步特殊化为正交普氏问题（Orthogonal Procrustes Problem）。首先对矩阵B T V进行SVD分解得到：

式中，∑=diag（σ1，σ2，…，σr）表示矩阵B T V的奇异值（singular values），而UL和UR分别表示左奇异向量和右奇异向量。因此，当B固定时，R的解可以表示为

本文提出的基于迭代量化的二值特征人脸识别算法的流程如表2-2所示。

表2-2　基于迭代量化的二值编码人脸识别算法流程