流体的流动分为层流流动（Laminar flow）和湍流流动（Turbulent flow）。从试验的角度来看，层流流动就是流体层与层之间相互没有任何干扰，层与层之间既没有质量的传递也没有动量的传递；而湍流流动中层与层之间相互有干扰，而且干扰的力度还会随着流动而加大，层与层之间既有质量的传递又有动量的传递。
判断流动是层流还是湍流，是看其雷诺数是否超过临界雷诺数。雷诺数的定义如下：
式中，V为截面的平均速度；L为特征长度；ν为流体的运动黏度。对于圆形管内流动，特征长度L取圆管的直径d。一般认为临界雷诺数为2320，即
当Re＜2320时，管中是层流；当Re＞2320时，管中是湍流。
对于异型管道内的流动，特征长度取水力直径dH，则雷诺数的表达式为
异型管道水力直径的定义如下：
(www.xing528.com)
式中，A为过流断面的面积；S为过流断面上流体与固体接触的周长。临界雷诺数根据形状的不同而有所差别。
层流求解相对简单，虽然N-S方程能够准确地描述湍流运动的细节，但运用直接数值模拟法（DNS）求解这样一个复杂的方程会花费大量的精力和时间。实际上往往对湍流建立模型来描述工程和物理学问题中遇到的湍流运动。
湍流计算模型定义：从工学的角度，对湍流流动进行某些适当的简化处理，使流场的复杂度得到一定程度的缓和，从而在现有计算资源的条件下也能大致上表征出流场的特点。湍流计算模型大致分为两类：一类为空间筛滤方法，代表为大涡模拟LES模型；一类为系综平均化方法，代表为RANS模型。从模型的基本出发点，把这几类主要模型做比较，从表中可以看出来看，RANS更适合工程实际应用，见表15-1。
表15-1 DNS、LES、RANS模型的基本区别
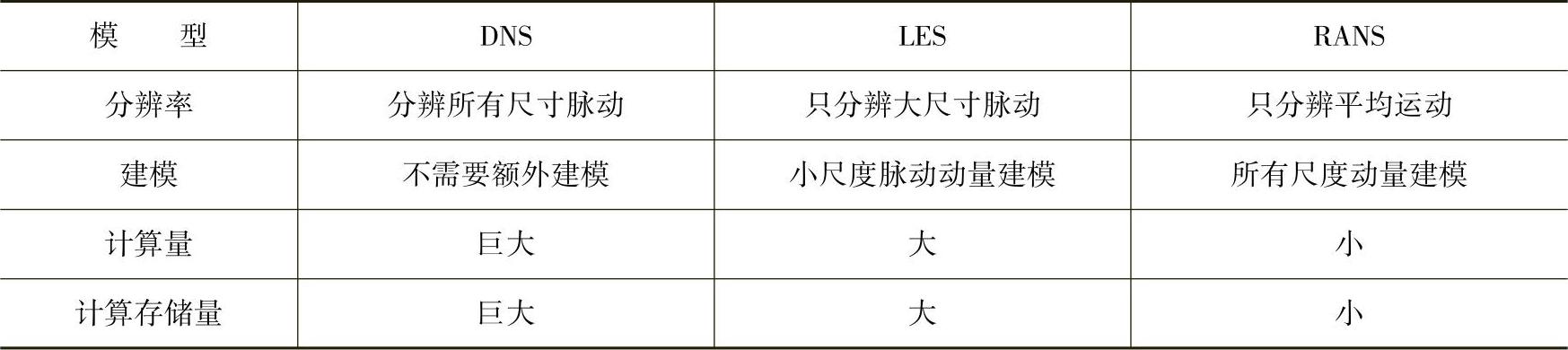
CFD模拟的难点之一是湍流模型的选用。目前存在大量的湍流模型，这些湍流模型是根据不同的问题进行修正的结果。每个湍流模型有相应的特点和适用范围，应根据不同的问题，选择合适的湍流模型。为了有个大致脉络，方便应用，把整个可压缩流体等温状态的湍流模型从建模方法上进行归类，如图15-1所示。具体方程数学形式和推导请参看相应专业书籍。
对于非等温问题，可压缩的流动，如两相流问题、自由表面流动、建筑扰流问题等都有相应的湍流模型，以及根据一些新问题提出新湍流模型。因此标准kε模型并不适合任何问题。
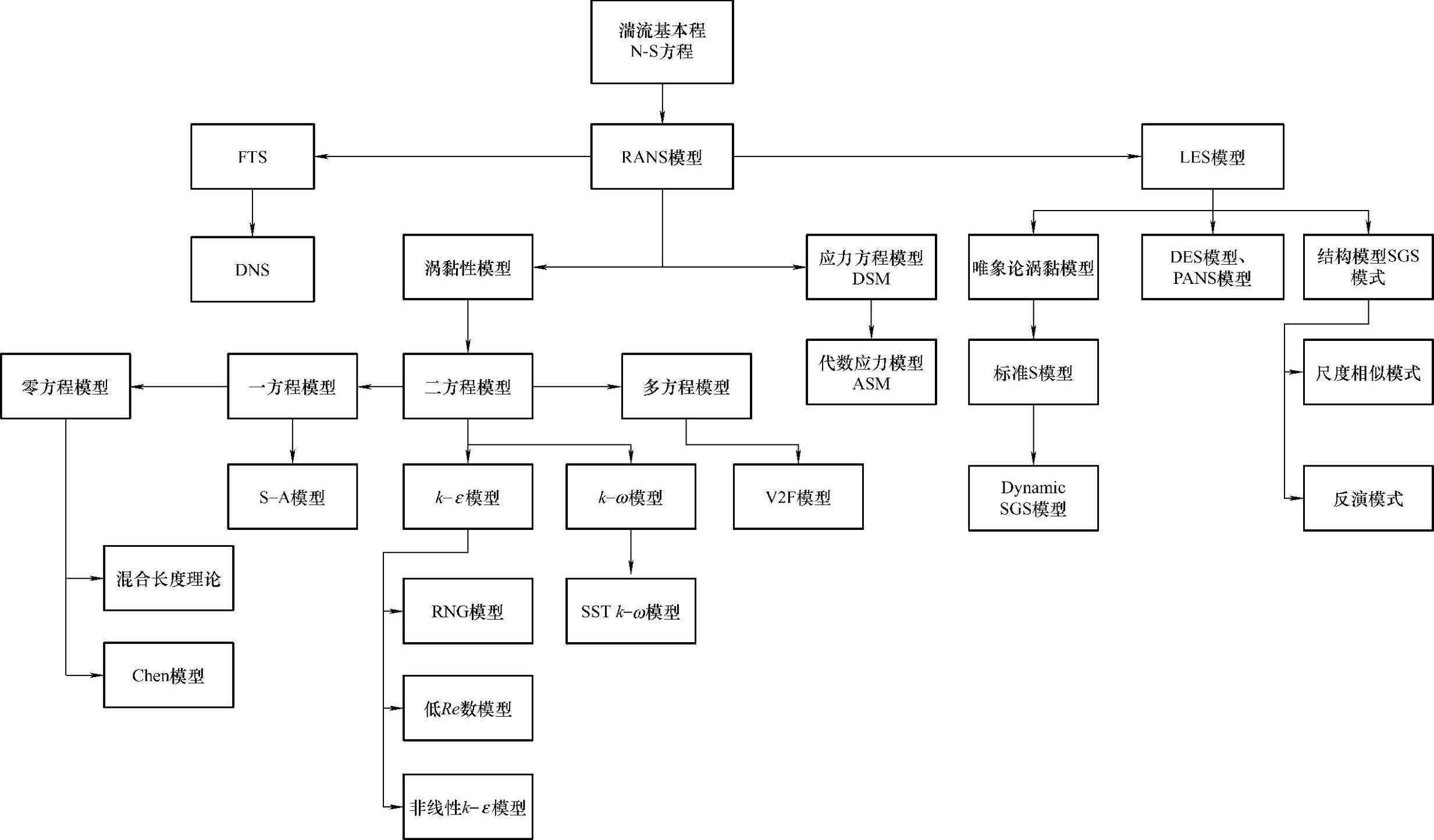
图15-1 湍流模犁
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
