有限元分析入门与应用：断裂力学参数

典型的断裂力学参数描述裂纹尖端前端的能量释放率或应力位移幅。其中应力强度因子、能量释放率、J积分是断裂力学分析常见参数，应力强度因子和能量释放率适用于线弹性断裂力学，J积分对线弹性和非线性弹塑性材料的断裂力学均适用。

1.J-积分

式中，W为应变能密度；T为动能密度；σ为应力；u为位移矢量；Γ为线积分域。

对于以线性弹性材料的裂纹，J积分表示的是能量释放速率。另外，裂纹尖端的应力和变形场的振幅的特征是J积分用于非线性弹性材料的裂纹。

2.应力强度因子

对于线弹性材料，裂纹尖端前面的应力应变区可表示为

式中，k是强度因子；r和θ是极坐标的坐标，如图12-3所示。

对Ⅰ型裂纹，应力场表述为

3.能量释放率

图12-3 裂纹尖端示意图

能量释放率裂纹由某一端点向前扩展一个单位长度时，薄板每单位厚度所释放出的能量。仅限于线弹性断裂力学，格尔菲斯首先提出并由欧文发展完善。

在断裂瞬间，能量释放率G等于临界释放率G_c。

对于单断裂模式，应力强度因子与能量释放率的关系：

对于平面应变问题：

平面应力问题：

E′=E （12-7）

式中，E是材料弹性模量；ν是泊松比。

4.材料力

材料力，也称构型力，主要用于分析如位错、孔洞材料缺陷、界面和裂缝等问题。

对一般的2D问题（不存在体积力、热应变和动态载荷情况下），节点材料力定义为

式中，ne为积分单元数；∑为Eshelby应力；N为形函数；▽N为形函数梯度。在小应变弹性范围内，引入Eshelby应力为

∑_ij=wδ_ij-▽u_ijσ_ij （12-9）(www.xing528.com)

式中，σ_ij为应力张量；▽u_ij为位移梯度；w为应变能密度；δ_ij为克罗内克符号。

在有限应变弹性范围内，Eshelby应力为

∑_ij=w₀δ_ij-F_ijP_ij （12-10）

式中，P_ij为第一皮奥拉 克希霍夫应力张量；F_ij为形变梯度；w₀为材料应变能密度。

如果存在塑性变形，材料体积力作用在域中表达式为

式中，B是材料体积力：

B=B^p+B^t （12-12）

B^p为塑性材料力。

B^p=σ·▽ε^p-q▽α （12-13）

式中，α为内变量系数；ε^p为塑性应变；q为关于内部变量的应变能密度扩展。

如果存在热应变，节点材料体积力向量为

B^t=ασ·▽θδ （12-14）

式中，α为热系数；▽θ为温度梯度。

对超弹性材料，材料力为

Eshelby应力为

∑=ψl-F^TP （12-16）

式中，ψ为超弹性势能。

5.T-应力

对线弹性材料，裂纹尖端附近应力场的渐近展开，以裂纹尖端为原点的局部极坐标表示为

在这里，涉及奇异项为应力强度因子，第一个非奇异项（T）为T应力。

T应力为平行于裂纹方向的应力。T应力与裂纹尖端应力三轴水平紧密联系，负T应力值表示降低裂纹尖端应力三轴水平（导致较大的塑性区），正T应力值表示裂纹尖端应力三轴水平（导致较小的塑性区）。

6.C∗积分

C∗积分用来评价均质材料经历二次（稳态）蠕变变形的裂纹尖端区域。C∗积分定义如下：

式中，σ_ij为应力张量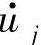；为位移率矢量；为应变能率密度；δ_ij为克罗内克符号；x_i为坐标轴；q为裂纹扩展矢量。