1.变形显示
在Mechanical的计算结果中,可以显示模型的变形量,常用的是总变形和各轴向变形,如图4-25所示。
1)总变形【Total Deformation】是一个标量,它由式
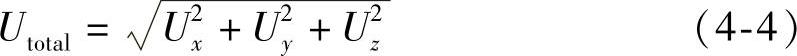
决定,变形结果对线、面、体都适用,变形结果仅和移动自由度有关。通常线和面的旋转自由度不能够直观地显示,但可以跟踪点的角度变化得到。
2)方向【Directional】可以指定给定坐标下的变形,如X、Y、Z方向的变形。

图4-25 变形量分析选项
3)总的速度【Total Velocity】、总加速度【Total Acceleration】及方向分量仅在瞬态结构动力分析、刚体动力分析、随机动力分析及频谱分析时可用,其中方向分量仅在随机动力分析及频谱分析时可用,详细介绍可参看相关章节。
2.应力和应变显示
在Mechanical的计算结果中,可以显示模型的应力和应变,见表4-2。应变【Strain】是弹性应变。应力【Stress】和弹性应变都是张量,并且分别有6个分量(X、Y、Z、XY、YZ、XZ),而热应变可以看作一个带有3个分量(X、Y、Z)的矢量。
表4-2 应变应力结果

(1)等效应力/等效应变 等效应力和主应力的关系可表示为
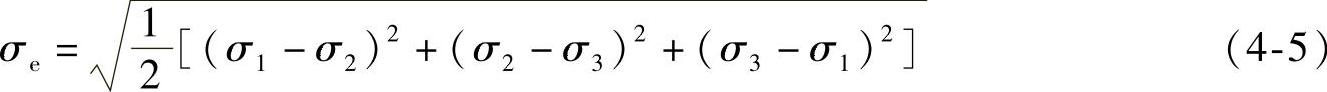
等效应力也称Mises等效应力,它遵循材料力学第四强度理论(形状改变比能理论)。它用应力等高线来表示模型内部的应力分布情况,可以清晰描述出一种结果在整个模型中的变化,从而可以快速地确定模型中的最危险区域。等效应力是一种利用不变标量来实现得到单轴晶体应力状态的普遍方法。
等效应变的计算公式如下:
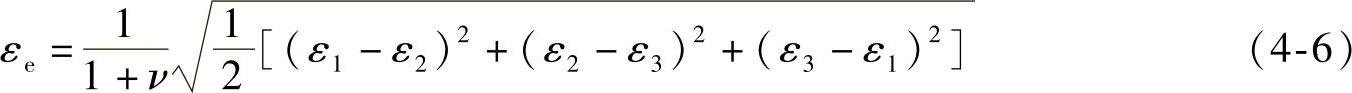
式中,ν为泊松比。
(2)主应力/主应变 主应力【Maximum Principal Stress】为物体内任一点剪应力为零的截面上的正应力。做结构设计时,有时是以主应力为设计指标。最大主应力是用来描述结构的实际受力情况,它的大小决定了结构是否出现裂缝和受剪切破坏。方向就是实际破坏面的方向。
主应变【Maximum Principal Strain】是指应变椭球体主轴方向的应变。(https://www.xing528.com)
(3)主应变/应力向量 主应力和主应变可以被指定,三个主应力值带有方向,因此可以利用主应变/应力向量【Vector Principal】选择指定。
(4)热应变 热应变【Thermal Strain】是在结构分析中指定热膨胀系数并施加温度载荷后计算所得,求解前需在对象的详细窗口栏中选取【Thermal Strain Effects】为Yes。对于热应变,仅对壳体和实体适用。
(5)薄膜应力 薄膜应力【Membrane Stress】沿截面厚度均匀分布的应力成分,它等于沿着所考虑截面厚度的应力平均值。由无力矩理论求解的壳体应力均为薄膜应力,且属一次薄膜应力。根据有力矩理论计算,不连续应力中也含有薄膜应力分量,但属二次应力。由于薄膜应力存在于整个壁厚,一旦发生屈服就会出现整个壁厚的塑性变形。在压力容器中,其危害性大于同等数值的弯曲应力。
(6)误差结果 误差结果【Error】可以帮助用户确定求解应力结果收敛情况及网格细化,如高误差点与最大应力集中点位置远近可判断结果是否收敛。误差结果对线性应力结果有效。
(7)积分点的结果显示 积分点的结果显示选项包含了非均匀化的节点解【Unaver-aged】、均匀化后的节点解【Averaged】、节点的最大差值解【Nodal Difference】、节点分数解【Nodal Fraction】、单元内部节点的最大差值解【Elemental Difference】、单元内部节点的分数解【Elemental Fraction】、单元内部节点的平均解【Elemental Mean】,如图4-26所示,它们之间的关系如图4-27所示。其中【Averaged】是默认选项,可以均匀化共享的单元节点及不连续几何的节点;通过选项【Average Across Bodies】来确定。

图4-26 积分点的结果显示

图4-27 积分点的结果关系图
1)非平均化的应力【Unaveraged】,在单元内部基于积分点的解是根据形函数推算出的该单元几个节点的解,如果一个节点周围毗邻几个单元,则这几个单元在同一节点处会出现不同的解。这里的解是最初计算出的结果,相对比较真实准确,是进行结果考察的主要依据。
2)平均化的应力【Averaged】,对所有单元进行计算并得到其节点的解,对于共享节点,对该点的几个解均匀化,得到该点的唯一解。用于获取某一节点解。
3)节点应力差的最大值【Nodal Difference】,对所有单元没有均匀化的解,共享节点的解先排序,得到最大最小值,然后由最大值减去最小值即为该节点解。对于应力显示,它反映了应力梯度在哪个节点上最大,也是应力集中发生的地方,是细化网格的依据。
4)节点应力误差【Nodal Fraction】,该值由Nodal Difference解除以Averaged解得到,是一种相对误差的概念,表示当节点取得平均解后,其误差的多少。该值的绝对值越大,预示着均匀化导致的误差就越大,是选取平均值的一个判断依据。
5)单元应力差梯度【Elemental Difference】,在一个单元内的所有节点,先找到单元内部节点解的最大最小值,然后由最大值减去最小值即为该节点解。对于应力显示,它反映单元内部的应力梯度,该值越大,意味着该单元自身内部应力变化很大,也预示着该单元应该进一步细分才能得到更正确的结果,是细化网格的依据。
6)单元内部节点平均【Elemental Mean】,在一个单元内部,在节点的值平均后,对于单元内所有的节点再均匀化,得到单元内部的节点平均解。用于获取某一单元解。
7)单元应力平均误差【Elemental Fraction】,在一个单元内部,该值由Elemental Differ-ence除以Elemental Mean解得到,是一个相对误差的概念,表明单元取得平均值后的误差。该值的绝对值越大,预示着单元值均匀化后导致的单元解误差就越大,是选取平均值的一个判定。
3.梁结果
梁的结果适用于由线体构造的梁或管道单元分析结果处理。求解工具栏中的梁的结果选项见表4-3。
表4-3 梁结果

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




