SolidWorks®Simulation：h自适应选项

用上述设置求解该算例将会发生什么？SolidWorks Simulation将会数次求解相同模型，每次将使用更精细的网格。细化网格将自动进行，无须用户介入。

网格将被细化几次？考虑到设置了【最大循环数】为【5】，SolidWorks Simulation将求解原始网格然后完成数次网格细化。循环将在满足【目标精度】或【最大循环数】达到5后停止，这意味着求解将最多由6步构成：原始网格和5次细化。

【目标精度】是模型总体应变能标准（RMS应变能）的精度。本例将其设置为98%意味着在两次连续循环总体应变能差值低于2%时停止。

1.目标精度 【目标精度】基于模型的整体应变能，是离散化误差的整体度量。它对局部误差不敏感，即便局部误差很大。

2.精度偏差 为说明局部误差，循环也需要用【精度偏差】控制。可以将【精度偏差】滑块置于左端（【本地】）来让程序获得峰值应力结果，意味着本地（局部）区域具有高应变能误差，将被“优先处理”（在这些区域网格将被高度细化）。还可以把滑块移至右端（【整体】）来让程序获得相对低的应变能误差，不必直接控制全部应变能的数量。

从第2章可知，应力奇异发生在集中载荷和尖锐凹角区域。当使用细小的网格单元时，这些区域的应力偏离到无限大。

故对于有这样奇异点的模型，推荐将【精度偏差】滑块移至右端（【整体】）。这种办法可以忽略局部应变能误差，解算器无须调节网格细化模式来减少这些误差。【本地精度偏差】通常比【整体精度偏差】更快地得到结果。

用【h-自适应】求解，可从粗糙的原始尺寸网格开始。该网格作为起始点，在求解过程中Solid_- Works Simulation可对其进行精细划分。此外，在细化网格过程中如果选择【网格粗糙化】，正如在这个算例中设置的，网格将被“粗糙化”。

假如【h-自适应】解算器认为初始的网格“过分细化”，在一些位置网格可以变得粗些，这意味着在这些位置的过分细化仅会稍微降低该处的应力梯度。

网格无须统一进行细化，仅需要细化部分区域以降低应变能误差。可以说网格自动适应于应力状况，故将h-自适应求解方法称为“自适应”。网格对比如图13-10所示。

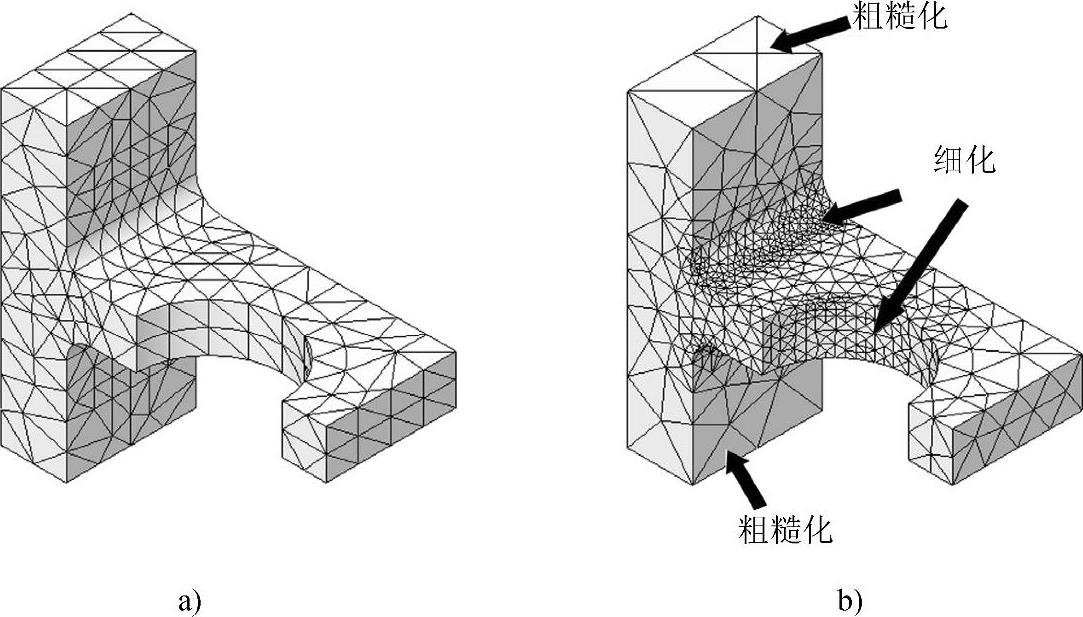
图13-10 网格对比

a）原始网格 b）采用h-自适应方法后的网格

步骤11 对算例h-adaptive创建网格

将网格密度滑条拖至粗糙单元对模型划分网格，确认使用【高】品质单元，如图13-11所示。因为没有足够多的单元来获取圆角附近复杂的应力梯度，故该网格不适用于标准求解技术。(www.xing528.com)

步骤12 运行h-adaptive算例

运行h-adaptive算例。注意到每步的解算过程对应于网格细化次数。为帮助查看应力结果，材料屈服的地方将以不同颜色图解显示。

步骤13 对屈服区域设置不同颜色

在Simulation菜单中选择【选项】，进入【默认选项】选项，选择【图解】下的【颜色图表】。

勾选【为vonMises图解指定大于屈服力的值的颜色】复选框。注意默认的颜色为灰色，然后单击【确定】，如图13-12所示。

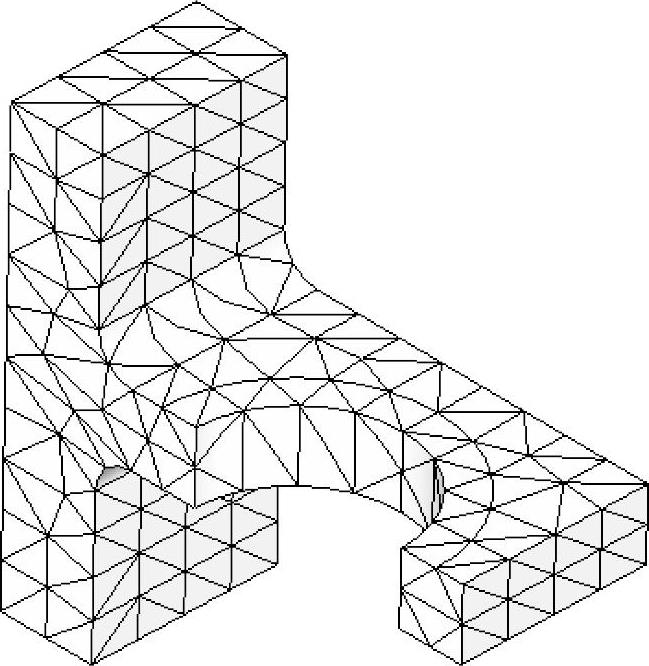
图13-11 粗糙网格

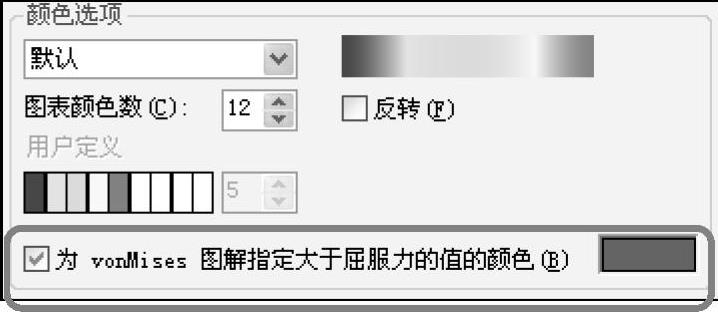
图13-12 设定屈服区域颜色

步骤14 图解显示von Mises应力

定义一个新的von Mises应力图解。在【设定】对话框中，【边界选项】设定为【网格】，结果如图13-13所示。

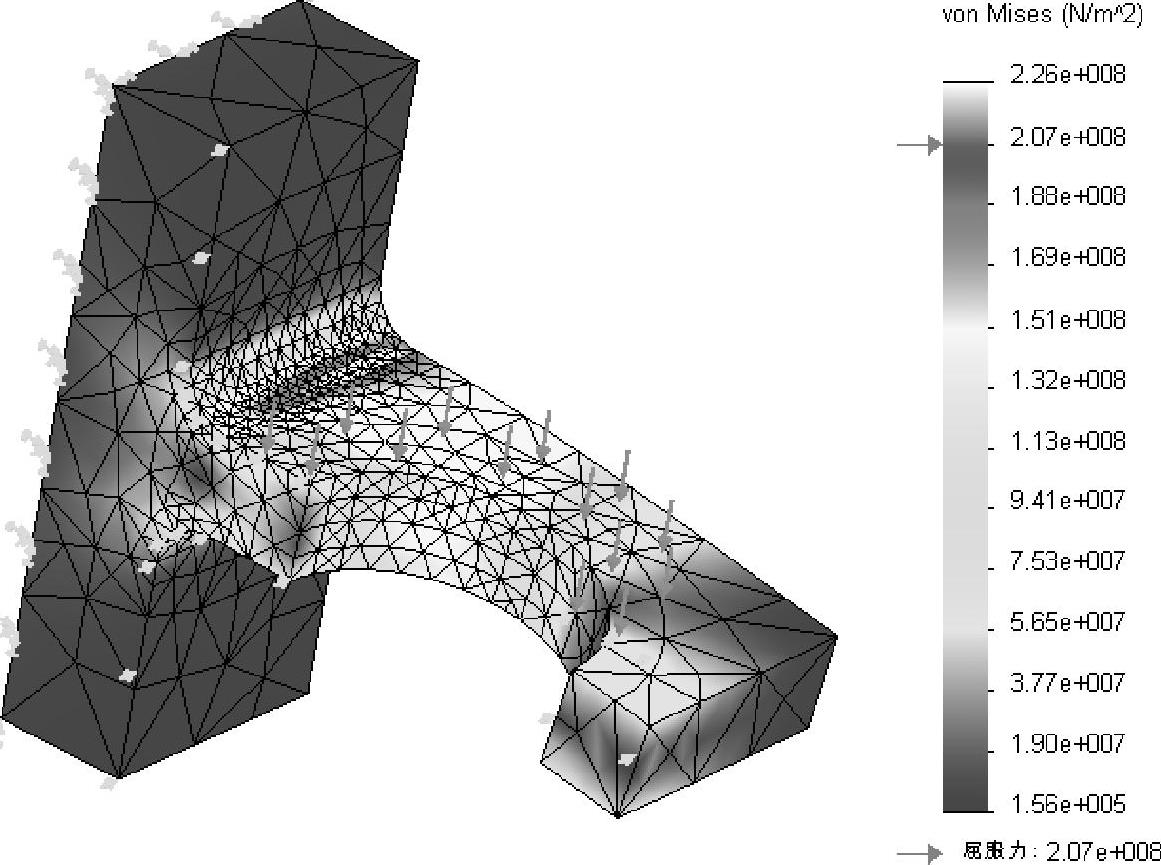
图13-13 应力结果显示

应力图解显示最大von Mises应力值为226MPa，稍高于材料AISI 304 steel的屈服强度。注意，屈服的区域以不同颜色显示出来。查看带网格显示的图解，确认在应力集中处确实进行了细化，并在模型“应力均布”的地方进行了网格粗糙化。