注意对支架的几何形状作了简化以便于网格划分,外部的装饰圈已经被压缩了。尽管这些细节并不足以复杂到使划分网格或求解产生困难的程度,但这样做是为了强调对于复杂模型而言简化经常是必须的。
1.对称 由于支架的几何形状、载荷和支撑的对称性,可以只取1/2的模型以简化有限元模型,如图13-3所示。
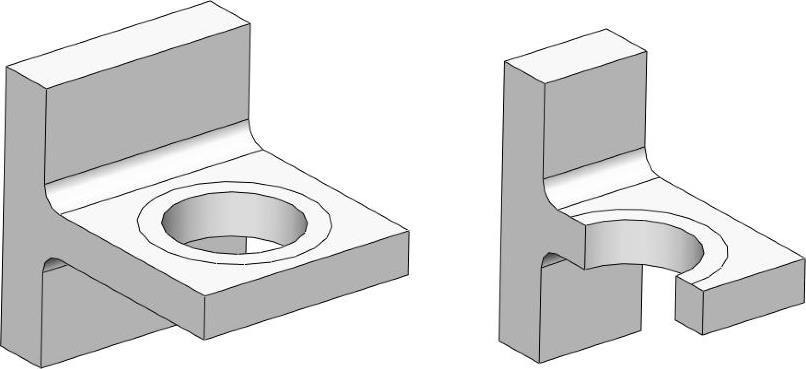
图13-3 对称模型
步骤3 创建算例
创建一个名为“standard”的静应力分析算例。当比较不同的求解方法时,这个算例将提供一个参考结果。算例名称“standard”反映了使用“常规”解决方法,即解算过程中网格不发生变化。这也是本培训教程前面几章使用的方法。
材料属性(AISI 304)已经在SolidWorks中预先定义并经过SolidWorks Simulation自动转换得到。
步骤4 施加载荷
在孔周围的分割面施加11000N的力,如图13-4所示。注意仅施加一半大小的力,因为模型只是原几何体的一半。
步骤5 在支架背面施加固定几何体的夹具(见图13-5)
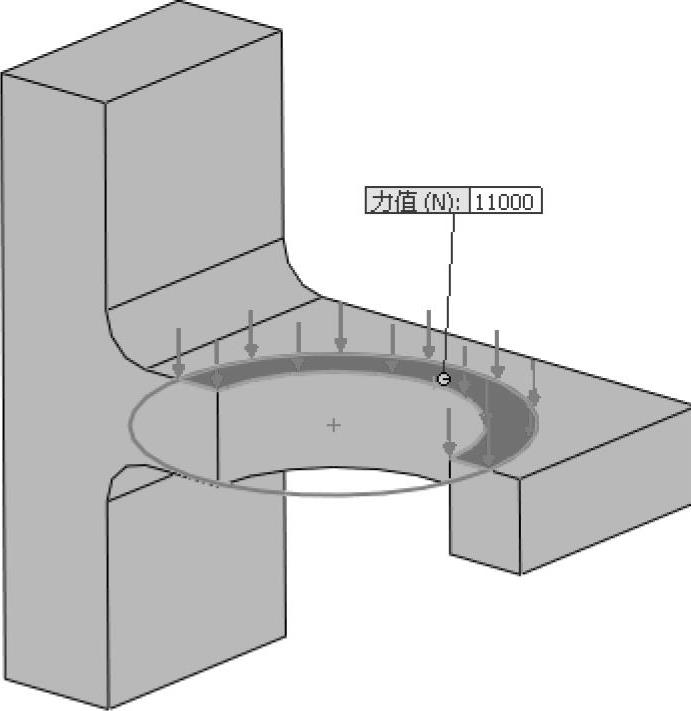
图13-4 施加载荷
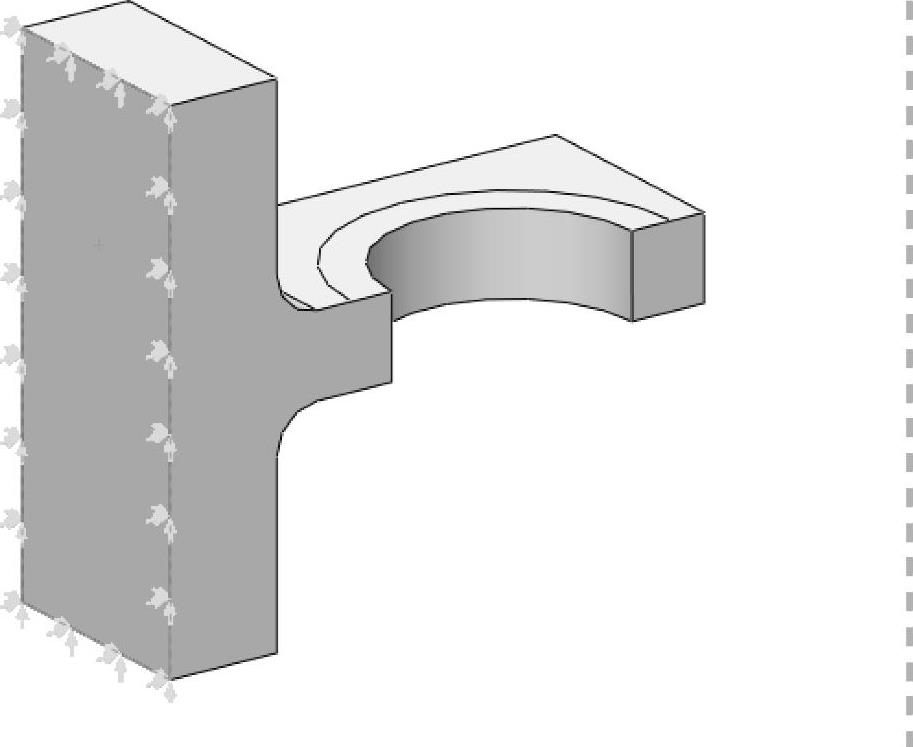
图13-5 施加约束
步骤6 施加对称边界条件
对剖面施加【对称】边界条件,如图13-6所示。
步骤7 划分算例standard中的网格
使用默认单元大小生成【高】品质单元网格,使用【基于曲率的网格】,如图13-7所示。(https://www.xing528.com)
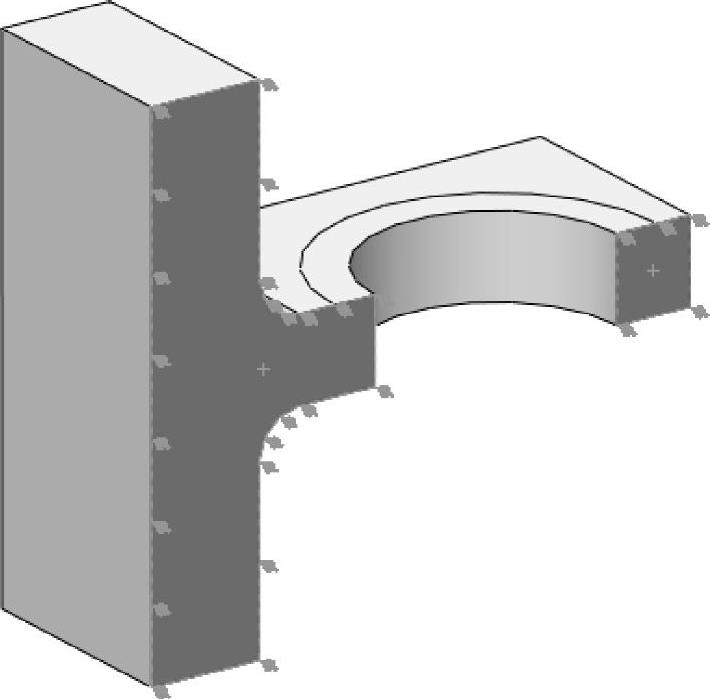
图13-6 施加对称边界条件
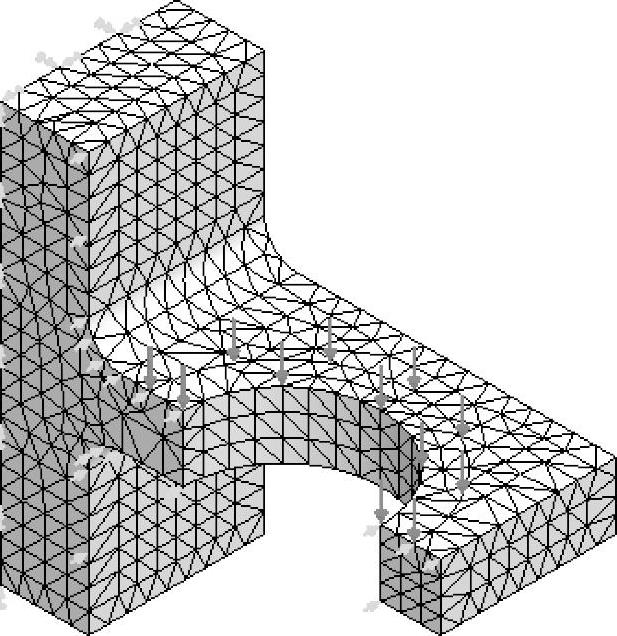
图13-7 划分网格
注意这里采用均匀单一的单元大小,不需要定义局部网格控制。
步骤8 运行分析
对算例“standard”运行求解。为验证预期的对称边界条件,动画显示一个结果图解。当模型变形时,确认施加对称边界条件的面恒为平面,且在对称平面的法向上无移动。
2.h-自适应求解方法 在解释【h-自适应】求解方法前,应了解有限元分析的结果依赖于模型是如何划分网格的。
从前面的观察可知,有限元分析所关心的焦点是离散方法的选择。因此,改变网格参数(全局或局部网格控制)将影响有限元分析结果。这是因为不同的网格(不同的离散选项)会导致不同的离散误差。
离散误差可以通过系统化地改变网格,并研究对感兴趣区域的影响来估计。这一过程称为“收敛过程”。
一种网格系统变换的方法是通过细化网格改变单元格尺寸来实现的。因为h表示单元尺寸特征,所以通过网格细化的收敛过程称为“h收敛过程”,如图13-8所示。在该过程中,单元尺寸逐渐减小。
用户可以回顾在培训教程的第1章和第2章中介绍的h收敛过程。
在第1章中,均匀的细化模型意味着整个模型用相同尺寸的单元网格划分。在第2章中只在需要的地方用网格控制细化网格。
第1章与第2章中的收敛过程需要用不同的网格定义模型、运行分析和总结结果。这些练习可促进了解,但是单调乏味。现在使用【h-自适应】求解方法以自动进行h收敛过程。
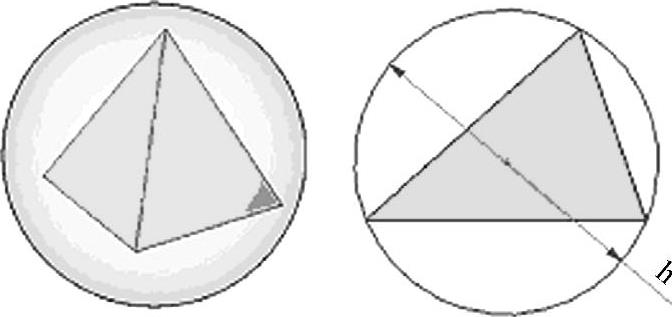
图13-8 h收敛过程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




