通过SolidWorks®Simulation，优化挠度

这个练习将采用设计情形的方法，计算出两个支撑点之间的距离，使得平板挠度最小。

本练习将应用以下技术：

● 设计情形。

● 多个设计算例。

● 设计情形结果。

● 设计算例图表。

1.项目描述 如图11-28所示，由塑性材料“尼龙6/10”做成的矩形平台（platform）由两根钢杆（Rod）支撑着。

注意到钢杆通过两块连杆（Link）悬挂着，而连杆本身为销钉（Pin）支撑，如图11-29所示。当矩形平台弯曲时，连接在矩形平台上的销钉之间的距离也会发生变化。

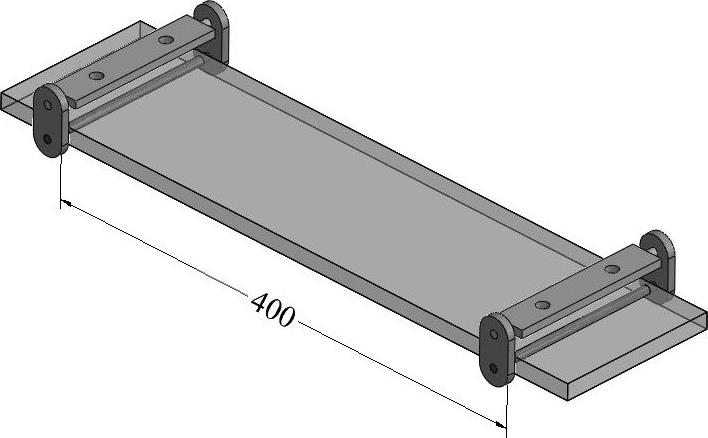
图11-28 矩形平台模型

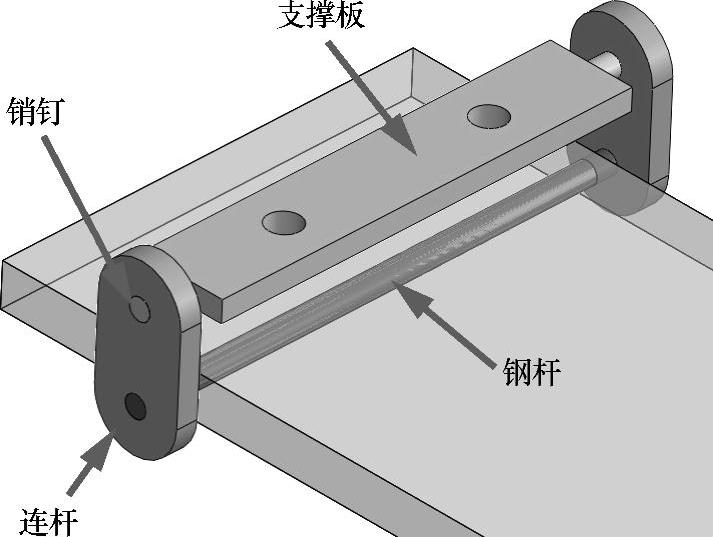
图11-29 矩形平台构件

这种支撑类型使得对矩形平台的挠度和应力算例可以采用线性模型分析。该矩形平台装配体承受100g加速度的激励。假设钢杆是刚性的，而且用户并不关注销钉和平板之间的接触。基于这些假设，可以将钢杆排除在分析之外。

因为钢杆可以通过适当的约束来取代，因此在分析中只需要使用SolidWorks的零件文件“plat-form”，而不是装配体文件“platform assembly”。

本例的目的是要找出两个钢销之间的距离以使矩形平台的挠度最小化。

2.平板分析

操作步骤

步骤1 打开文件

打开文件夹“SolidWorks Simulation\Lesson 11\Exercises\Platform-Design Scenarios”下的文件“platform.SLDPRT”。

步骤2 显示特征尺寸

在FeatureManager特征树中，右键单击【注释】并选择【显示特征尺寸】。

提示

本练习利用矩形平台的双向对称性来分析模型的1/4部分。

步骤3 创建对称切除

对特征“double symmetry”解除压缩。

步骤4 创建算例

创建一个名为“100G”的静应力分析算例。

步骤5 定义参数

在【插入】中选择【设计算例】/【参数】，或者在【评估】页面单击【参数】。在【参数】对话框中定义一个名为“distance”的参数。选择两点之间的距离尺寸为400mm，如图11-30所示。

步骤6 定义材料

在SolidWorks materials库中的【塑料】目录下，选择材料【尼龙6/10】。

图11-30 定义设计参数

步骤7 定义对称约束

在切除特征的两个表面上定义【对称】边界条件，如图11-31所示。

步骤8 施加约束模拟钢杆支撑

在圆柱孔面上应用【固定铰链】约束条件，如图11-32所示。

步骤9 施加重力载荷

施加重力载荷，右键单击【外部载荷】，并选择【引力】。选择Front基准面作为参考，

图11-31 定义对称约束

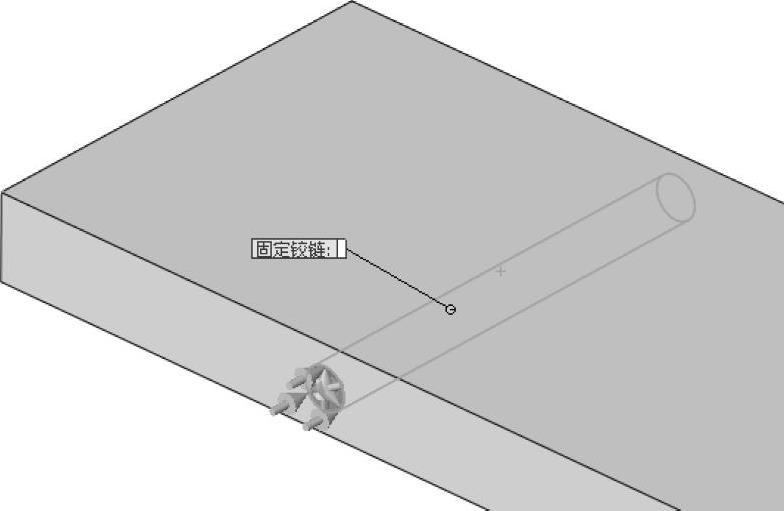
图11-32 施加铰链约束(www.xing528.com)

以定义重力加速度的方向。在【单位】选项中选择【SI（m/s²）】。

在Front基准面的法线方向输入981m/s²（该值为100倍的重力加速度），载荷沿Z轴负方向，如图11-33所示。单击【确定】。

图11-33 定义加速度载荷

提示

当加载重力时，质量密度是必须给出的材料属性。

步骤10 划分模型网格

使用默认设置生成【高】品质单元，使用【基于曲率的网格】。

步骤11 定义设计算例

定义10组设计情形并依次输入【distance】参数为475、425、375、325、275、225、175、125、75、25，单位为mm。

步骤12 结果指定

监视模型应力和合位移的全局最大值，以及图11-34所示两个顶点处相同变量的局部结果。

步骤13 运行设计算例

使用【高】品质网格。

步骤14 结果

查看von Mises应力和合位移的全局最大值，并查看顶点1位置和顶点2位置的局部应力和位移，如图11-35所示。

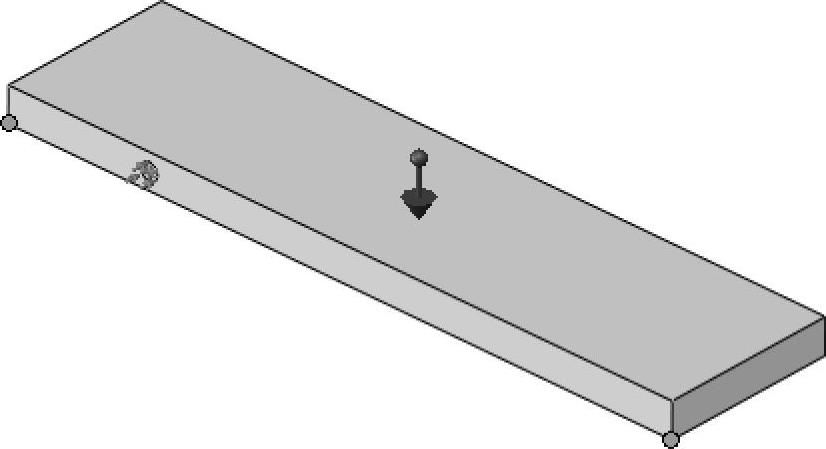
图11-34 结果指定

图11-35 设计算例结果

步骤15 以图表显示顶点1和顶点2的结果

定义设计历史图表，显示von Mises应力和合位移的变化，如图11-36所示。可以看到von Mises应力和合位移结果在支撑杆间距为275mm（5设置）时最小，分别对应4.7MPa和0.36mm。

步骤16 保存并关闭文件

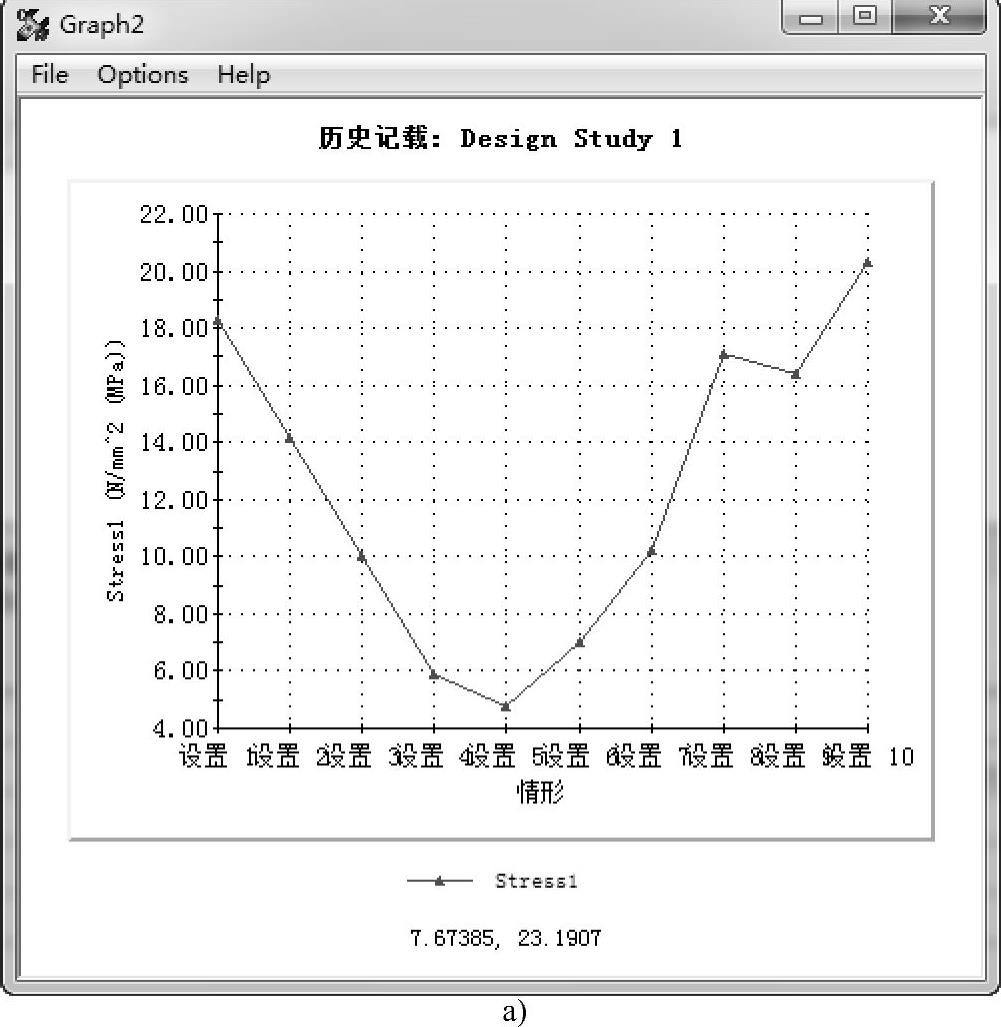
图11-36 von Mises应力和合位移结果

a）von MLises应力

图11-36 von Mises应力和合位移结果（续）

b）合位移

3.线性分析的局限性 练习开始就说明了该模型是通过浮动的连杆悬挂着的。这些连杆本身是由销钉支撑的，同时还能绕这些支撑销钉旋转。鉴于这个原因，当矩形平台在规定载荷下承受变形时，钢杆间的距离可能会发生改变。

因此在小变形的前提下，通过浮动的连杆而悬挂着的矩形平台不会产生拉应力，它仅仅靠弯曲应力来抵抗载荷，如图11-37所示。

如果连杆受到固定支撑，钢杆间也不能相互靠近，那么除了有弯曲应力以外，拉应力也会同时产生，如图11-38所示。

图11-37 旋转连杆产生拉应力

图11-38 固定连杆产生拉应力

这些拉应力又称为薄膜应力，是变形的结果，它将显著地增加矩形平台的刚度。

4.提问 这与线性分析有什么关系呢？

线性分析假设结构的刚度不随变形而发生变化，求解是基于在任何变形发生前计算的原始刚度。

因此，线性分析并没有考虑由薄膜应力而产生的附加刚度。这些薄膜应力是在变形过程中发生的。

即使想要模拟固定铰链叶，其解也仍会对应于浮动铰链，而矩形平台的刚度亦是偏低的。

为了区分浮动铰链与固定铰链，需要使用非线性几何分析，这些可在SolidWorks Simulation Premium中进行求解。