在本练习中,将分析一个水泵叶轮。由于模型中叶片和轮毂的厚度不同,将采用混合网格。
本练习将应用以下技术:
● 混合网格——实体和壳体。
● 接合壳体和实体网格。
● 定义抽壳厚度。
● 壳体和实体接合接触。
如图8-29所示,一水泵叶轮的转子以2000r/min的转速匀速转动。分析的目的是确定叶轮的位移和应力值。

图8-28 错误信息
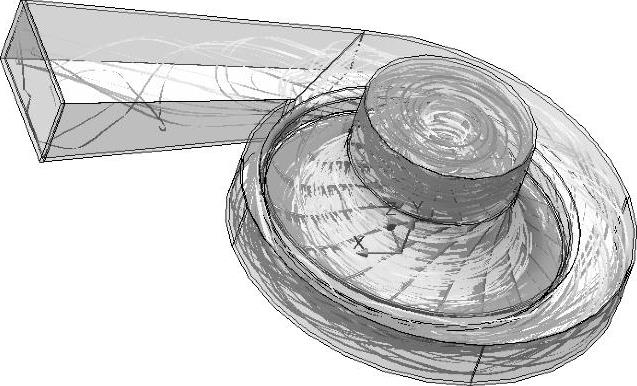
图8-29 水泵模型
在这种情况下,离心力对分析结果并不会有显著的影响,因此将被忽略。
操作步骤
步骤1 打开零件
打开文件夹“SolidWorks Simulation\Lesson 08\Exercises\Impeller-Mixed Mesh Analysis”下的“Lmpeller 01.SLDPRT”。
步骤2 创建算例
创建名为“centrifugal 01”的【静应力分析】算例,如图8-30所示。
步骤3 添加夹具
假定实体转轴与叶轮是刚性连接的。因此,为模拟该转轴,在叶轮的圆柱面上施加【固定几何体】边界条件,如图8-31所示。

图8-30 叶轮

图8-31 添加夹具
步骤4 添加载荷
在每一个叶片上施加8.9N的【法向力】,确认力的作用方向如图8-32所示。
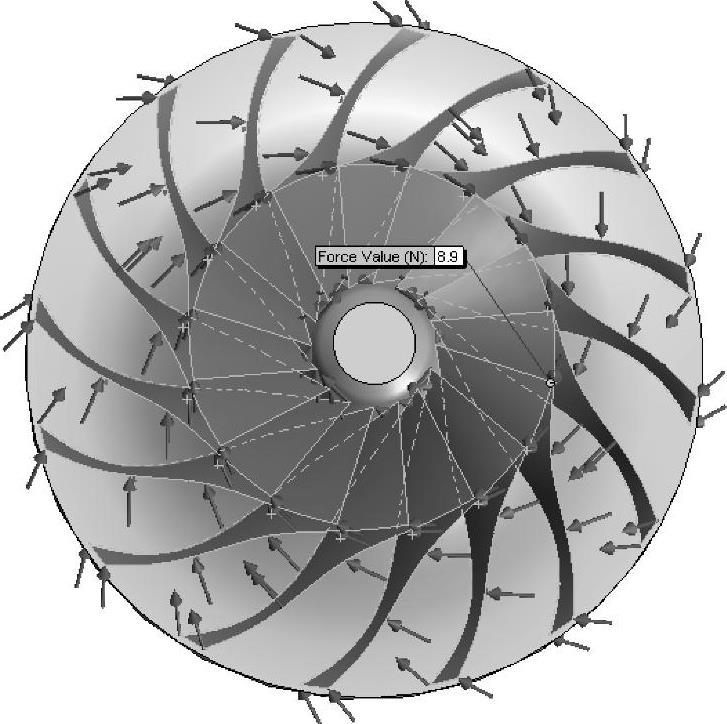
图8-32 添加载荷
提示
这个算例的压力合力是由SolidWorks Flow Simulation软件计算而得的。
步骤5 定义曲面壳体
使用叶轮的叶片曲面定义16个壳体特征,指定为【细】壳形式,【抽壳厚度】为1mm,如图8-33所示。
步骤6 指定材料属性
指定所有零部件材料为【合金钢】。
步骤7 应用网格控制
为了更精确地模拟壳体和叶轮实体之间的接合接触应力,在叶片边线上指定局部网格控制。其【单元大小】为2.5mm,【比率】为1.2,如图8-34所示。

图8-33 定义曲面壳体
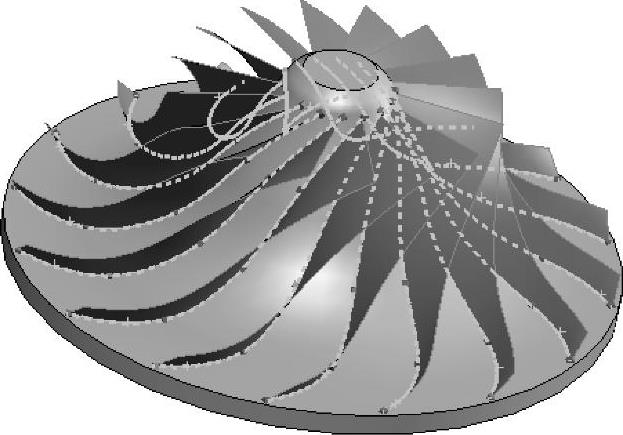
图8-34 应用网格控制
步骤8 定义叶片与叶轮实体接合接触条件
在叶片边线与叶轮实体上表面之间定义局部【接合】接触。指定16条叶片的边线为【组1】,叶轮实体上表面为【组2】,如图8-35所示。

图8-35 指定接触条件
提示
这里的全局接合接触设置是不重要的。可以看第8章的解释,模型的壳体和实体部分要求使用局部接触条件。
步骤9 生成网格
划分零件网格,选用【草稿】品质的【基于曲率的网格】,并使用默认设置,如图8-36所示。
步骤10 定义算例属性
指定用Direct Sparse解算器求解。
步骤11 运行分析
步骤12 图解显示径向位移
为显示径向位移结果,创建一个图解以显示【UX:X位移】。用模型的Axis1作为参考基准,UX便是径向位移分量。
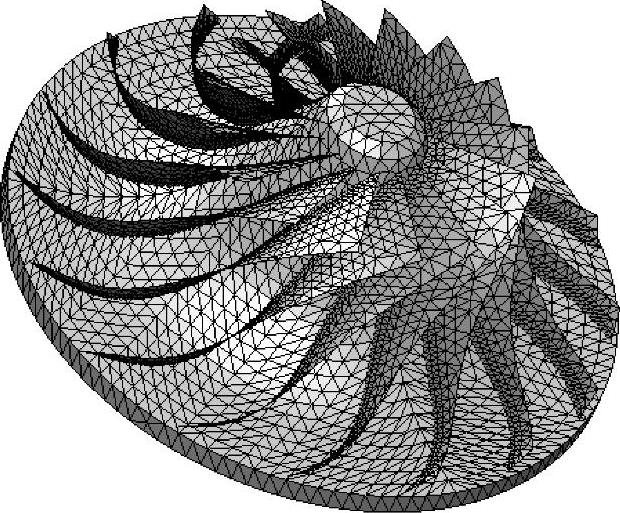
图8-36 生成网格
可以看到最大径向位移为-9.34×10-4 mm,出现在叶片的顶部,如图8-37所示。

图8-37 径向位移分布(https://www.xing528.com)
步骤13 图解显示von Mises应力
图解von Mises应力不需要使用任何几何基准,因为von Mises应力是标量应力值。使用剖视图来更好地显示支撑周围的应力结果,如图8-38所示。
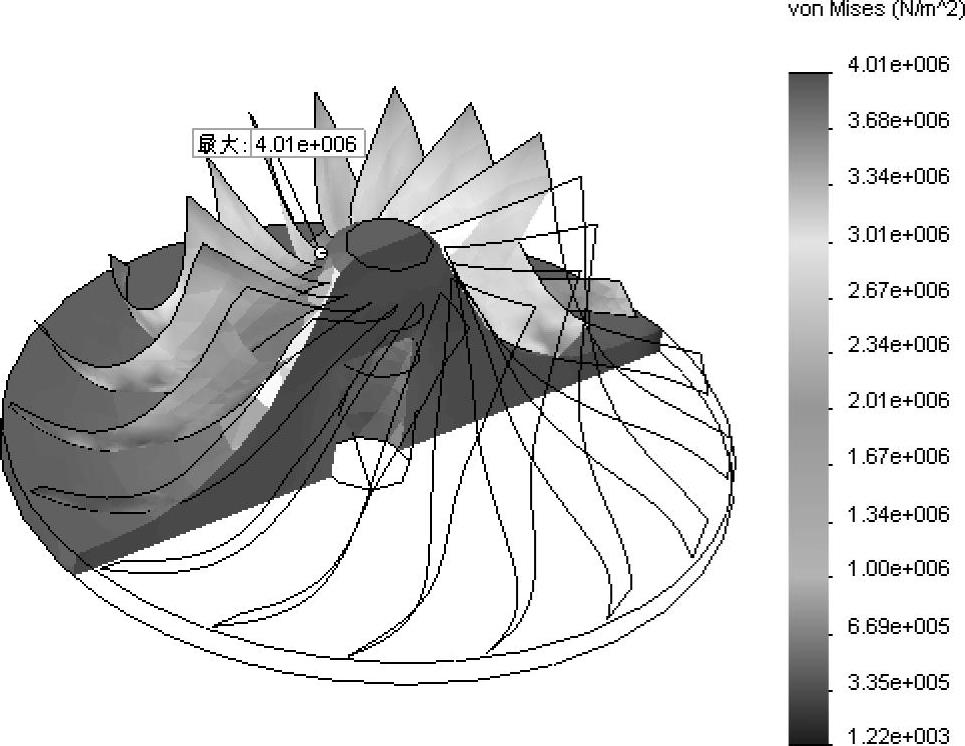
图8-38 von Mises应力分布的剖视图
可以看到非常小的von Mises应力值4.01MPa集中出现在叶片连接到实体的末端附近。由于存在焊缝,实际应力沿着接合边的分布是不同的。
当应力非常小时,位移结果对水泵叶轮零件间的加工间隙和使用效率显得非常重要。
为了获得精确的结果,需要用精细网格和高品质单元。这种详细的分析可能占用很多的求解时间,因此可以使用周期性对称模型来简化问题。
● 周期性对称 任何以沿着一根轴旋转生成的模型都可以认为是周期性对称的。所有这样的零部件都可以用周期性对称边界条件来方便地进行简化模型分析。类似的,所有可以使用一个草图绕着一根轴旋转形成的模型都可以称为轴对称。【周期性对称】约束用分析轴对称模型,即拥有切向载荷导致截面会发生垂直于平面的变形,如风扇的叶片。对于轴对称模型和径向载荷,应使用【对称】约束。
步骤14 激活配置periodicity
步骤15 创建算例
创建名为“periodicity”的【静应力分析】算例。
步骤16 排除曲面实体
除了SurfaceBody 4,将所有曲面实体排除在外。
步骤17 模拟转轴
在余下的叶轮圆柱面上施加【固定几何体】约束,如图8-39所示。
步骤18 模拟周期性
在一对切除面上定义【圆周对称】约束,使用【Axis1】为参考轴,如图8-40所示。

图8-39 模拟转轴
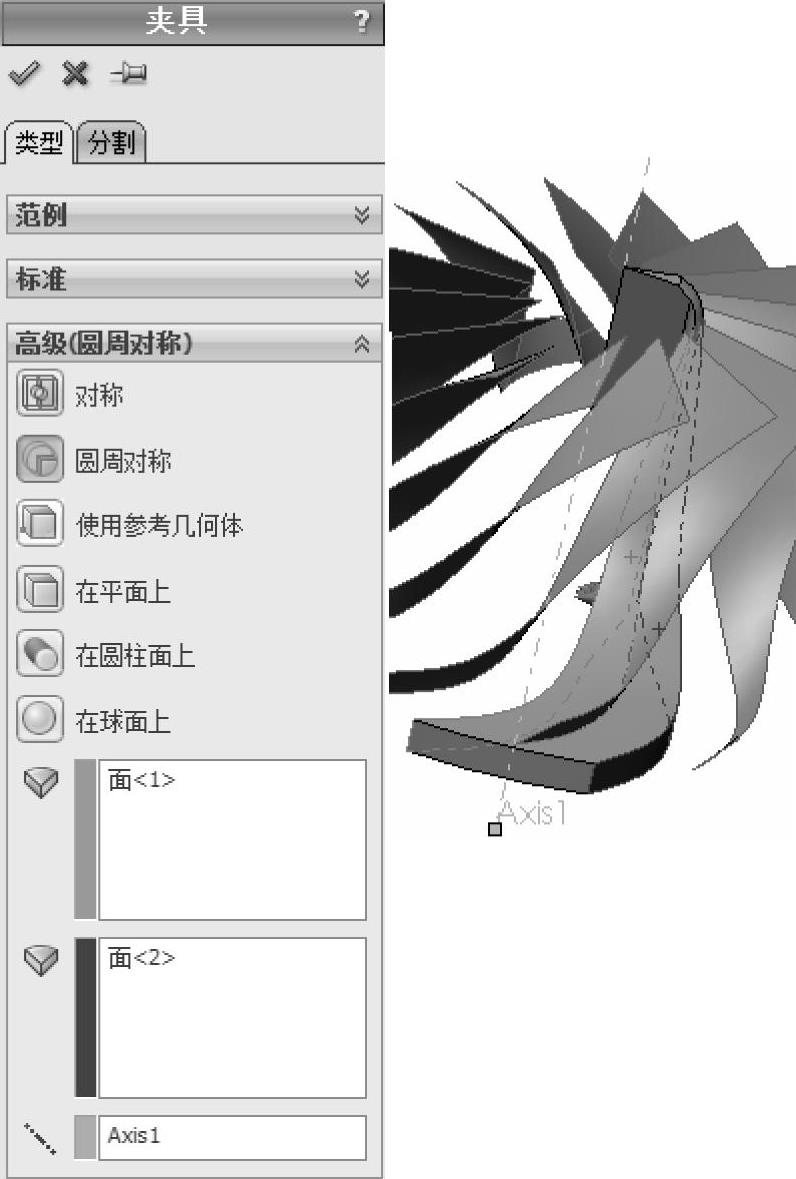
图8-40 指定圆周对称夹具
在剩下的两对切除面上定义相同的【圆周对称】约束,如图8-41所示。
步骤19 定义壳体特征
用与小块实体相接触的叶片曲面定义一个壳体特征,指定为【细】壳形式,【抽壳厚度】为1mm。在分析中不包括未使用的叶片。
步骤20 添加载荷
在定义壳体特征的叶片曲面上施加8.9N的【法向力】,确保力的方向与前一算例相同。
步骤21 指定材料属性
定义实体和壳体特征材料为【合金钢】。
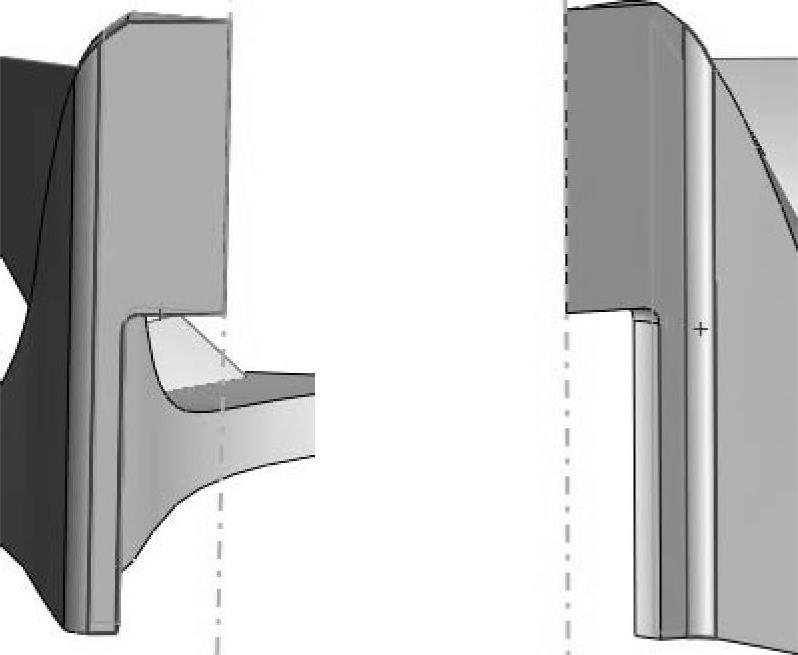
图8-41 对所选面定义周期性对称约束
步骤22 应用网格控制
在叶片曲面与叶轮实体上表面接触的边线上指定局部网格控制,使用【单元大小】为2mm,【比率】为1.2,如图8-42所示。
步骤23 对叶片与叶轮实体定义接触
同样的,在叶片边线与叶轮实体上表面之间定义局部【接合】接触,如图8-43所示。

图8-42 应用网格控制

图8-43 指定接触条件

图8-44 网格划分后的结果
步骤24 生成网格
在【网格参数】下选择【基于曲率的网格】。划分模型网格,使用【高】品质单元,保持默认设置,如图8-44所示。
步骤25 定义算例属性
指定用Direct Sparse解算器求解。
步骤26 运行分析
即便使用了【高】品质单元,也很快地完成了算例分析。
步骤27 图解显示径向位移
从图8-45中可以看到一个叶片顶点的最大径向位移变成-9.20×10-4mm,与用完整模型获得的径向位移相比有少量的下降。这个差异是由使用高品质单元及精细网格设置引起的,可以通过完整模型分析中的网格参数(草稿品质的粗糙网格)来验证结果是否一致。
步骤28 图解显示von Mises应力
从图8-46中同样可以看到局部的最大von Mises应力也有所改变。

图8-45 径向位移分布
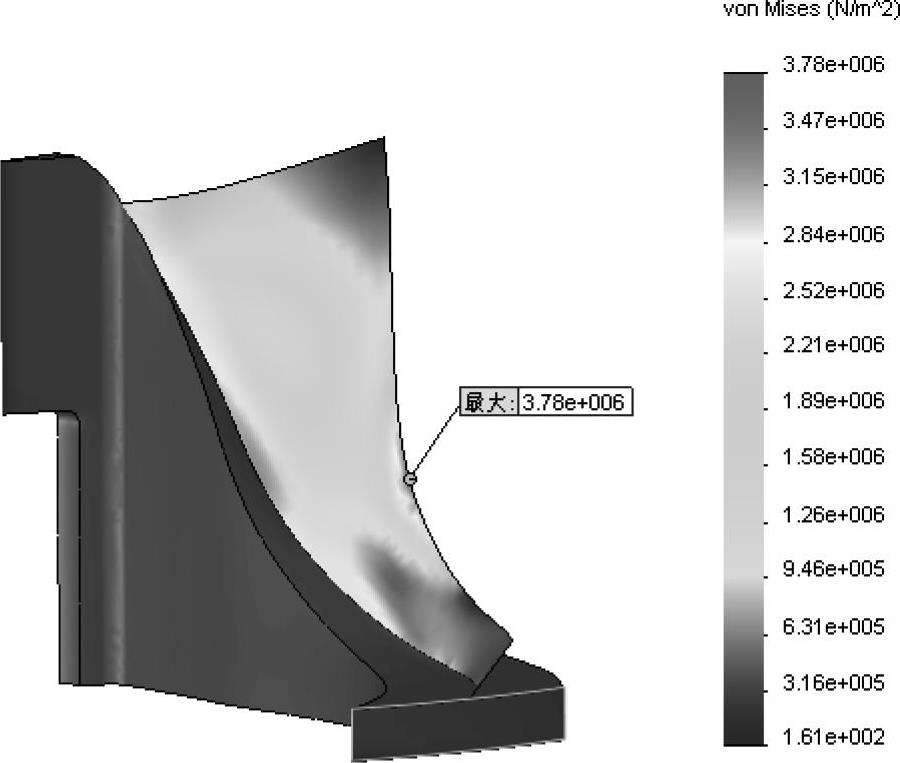
图8-46 von Mises应力分布
步骤29 保存并关闭文件
这个模型分析了叶轮的应力和位移。通常情况下,像这类叶轮的载荷都是周期性的(即动态变化的)。为了继续这个分析,用户可能需要求解系统的自然频率,以检验任何加载频率都不会影响动态响应。这可以使用SolidWorks Simulation Professional完成。此外,可以使用动力算例来求解全动态解,这可以使用SolidWorks Simulation Premium完成。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




