基础教程分析：搁栅吊件

对钣金特征而言，采用壳单元能够极大地简化工作。在这个实例中，将分析一个支撑楼房地板搁栅的钣金零件，如图7-39所示。每个地板搁栅在末端都由一个搁栅吊件相连接，因此可以只针对横梁的一半，采用对称的方法分析其中一个吊件。

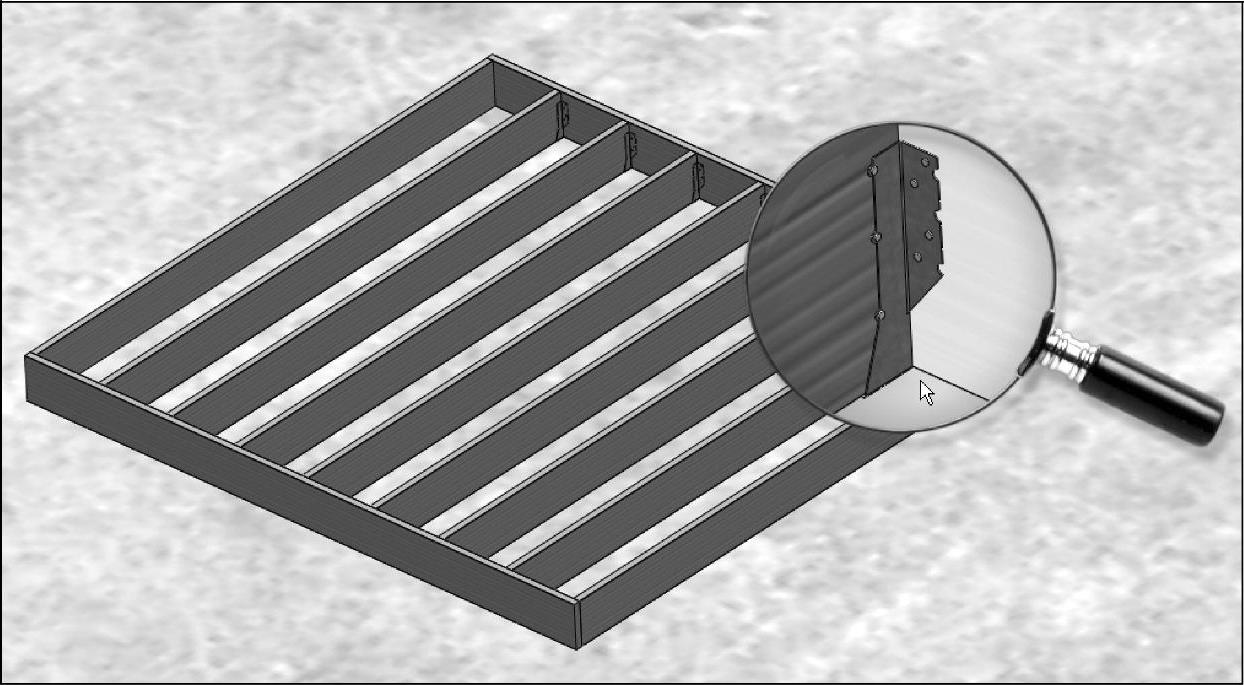
图7-39 搁栅吊件

搁栅吊件的背面钉入一块木方中。每个搁栅的末端都由一个搁栅吊件支撑，并钉入相应的位置，如图7-40所示。计算搁栅吊件和搁栅的最大应力及位移。

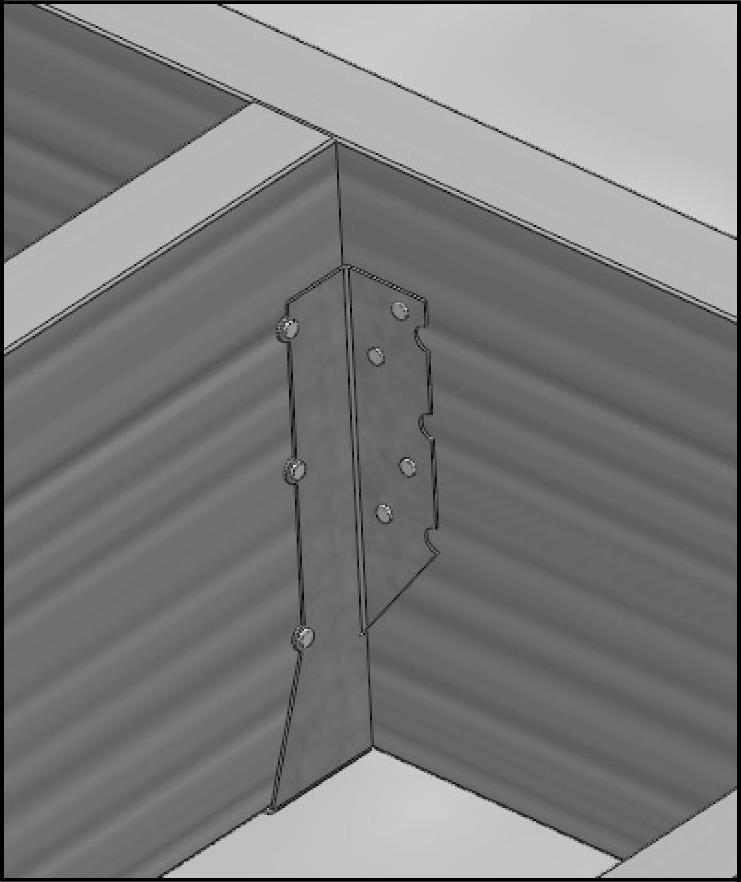
图7-40 吊件所处位置

操作步骤

步骤1 打开装配体文件

打开文件夹“SolidWorks Simulation\Lesson 07\Case Studies\Hanger Joist”下的文件“Floor Joist for Analysis”，这个装配体包含一个搁栅吊件以及半根横梁。

步骤2 创建算例

创建一个名为“floor joist”的静态算例。

步骤3 设定SolidWorks Simulation选项

设定全局单位系统为【公制（I）（MKS）】，【长度】单位为毫米，【应力】单位为N/mm²（MPa）。

步骤4 指定材料

对搁栅吊件指定材料Galvanized Steel。

步骤5 指定材料

对木质横梁指定材料。木材不是正交各向同性材料（在每个正交方向的材料属性相同），而是正交各向异性（在每个正交方向的材料属性不同）的，因此需要自定义材料和一些属性。

提示

现实中的木材是一种非常复杂的材料，正交各向异性的描述也并非贴切。因此将木材视为正交各向异性材料只是工程上的一个通常的简化方法，而得到的结果往往也是可接受的。

右键单击实体2×10beam-1（在零件下方）并选择【应用/编辑材料】，右键单击【自定义材料】文件夹并选择【新类别】，输入【Lesson 7 materials】作为新类别的名称。右键单击【Lesson 7 materials】并选择【新材料】，命名为Custom Wood。

在【模型类型】中选择【线性弹性正交各向异性】。现在就可以定义相对所选参考几何体的三个正交方向的材料常量。

选择“Front”基准面为参考几何体。本例中，这个选择使得全局坐标系中的X、Y、Z轴与材料对话框中的X、Y、Z相符合。全局坐标系中的X对应横梁的宽度，Y对应高度，Z对应长度。

如图7-41所示，输入【弹性模量】、【泊松比】、【抗剪模量】、【质量密度】的数值。在【屈服强度】中输入50N/mm²。单击【确定】。

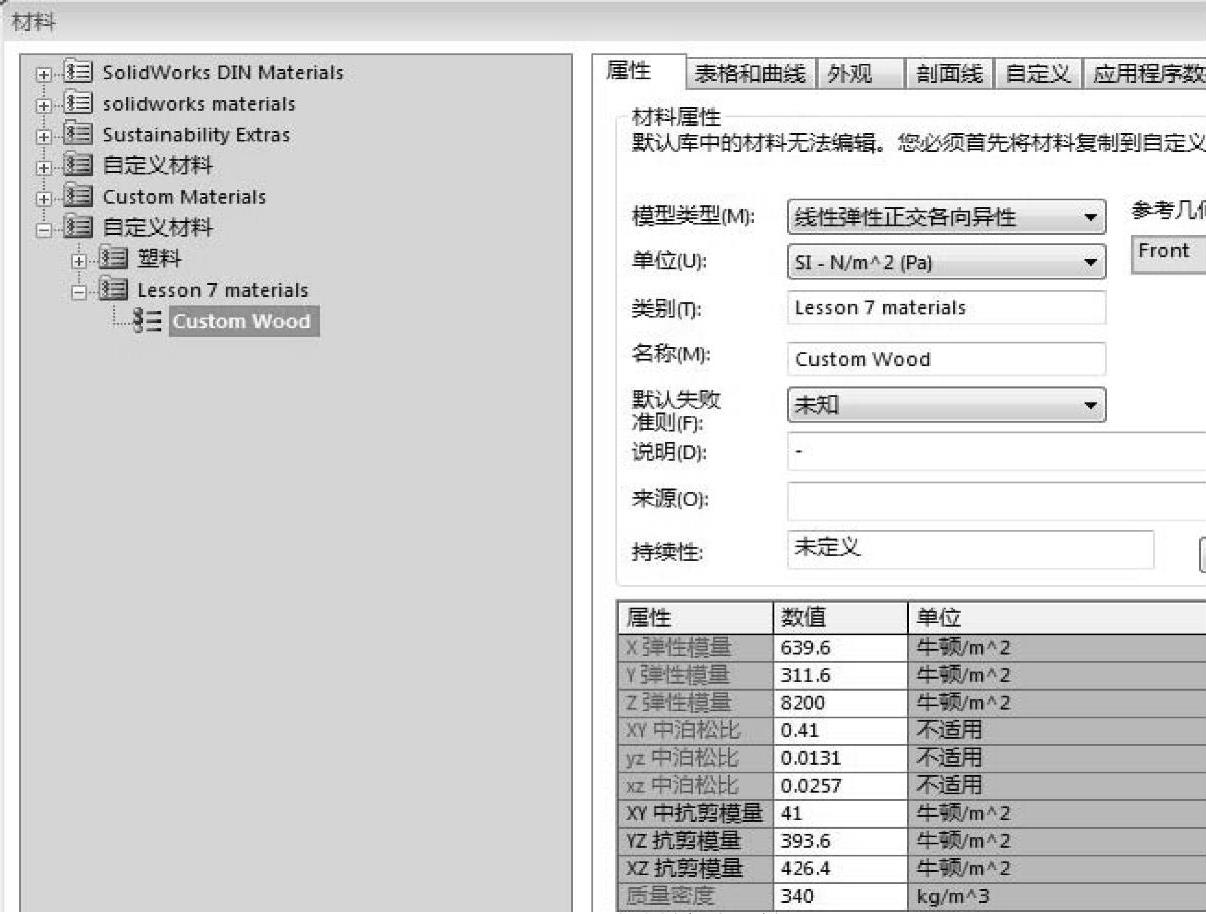
图7-41 指定材料

提示

确保以正确的单位N/mm²（MPa）输入所有材料数据。

步骤6 设置全局接触

编辑顶层装配体零部件接触（全局接触），并改为【无穿透】类型。

提示

零部件接触适用于这种情形，因为实体零部件的表面互相接触。一般来说，带有间隙的网格接触必须借助于局部接触条件。

步骤7 添加夹具

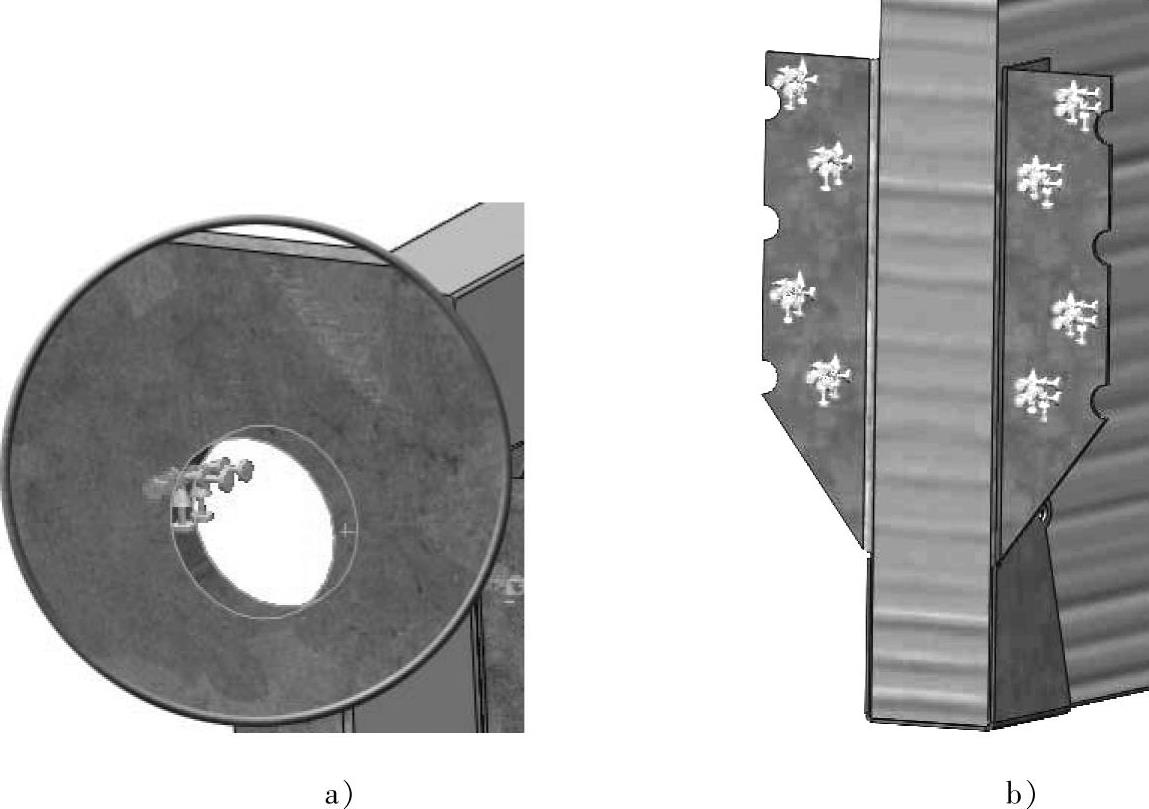
吊件是钉入到了头横梁的，因此在吊件背面的八个柱形孔中添加【固定几何体】的约束，如图7-42所示。因为模型是钣金，请确定选择的是面而不是孔的边线。这个夹具会自动匹配到钣金边线。

步骤8 添加对称的边界条件

在横梁末端添加一个【对称】的夹具，如图7-43所示。

(www.xing528.com)

图7-42 添加固定约束

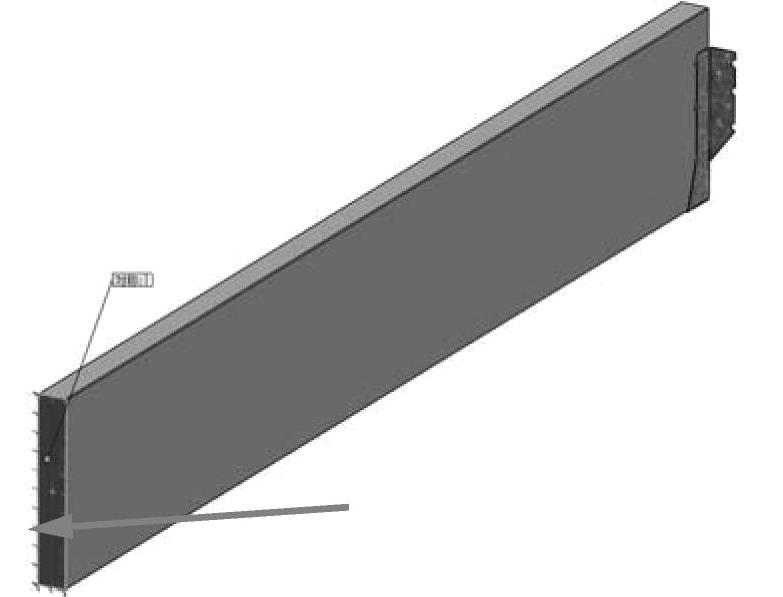
图7-43 添加对称的边界条件

● 钉子的作用 用户必须指定接头的刚度。搁栅横梁的钉子肯定会增加接头的刚度。然而，横梁是在钉入钉子之前放置在搁栅上的，因此在垂直方向上，几乎所有的载荷都通过底部承载面传递到搁栅上了。钉子增加的刚度实际上减小了木质横梁的真实变形，然而这并不是本章的主题。我们的目标是评估搁栅的性能，也就是传递所有载荷，然后提供更具现实意义的、保守的解。

步骤9 添加外部载荷

对横梁顶面添加500N的力。由于分析的对象只有半个梁，因此对应的整个梁上的载荷应该是1000N，如图7-44所示。

步骤10 划分网格

在【网格参数】下选择【基于曲率的网格】，将单元大小的滑块移到最右端，使用【草稿】质量的单元划分网格，结果如图7-45所示。

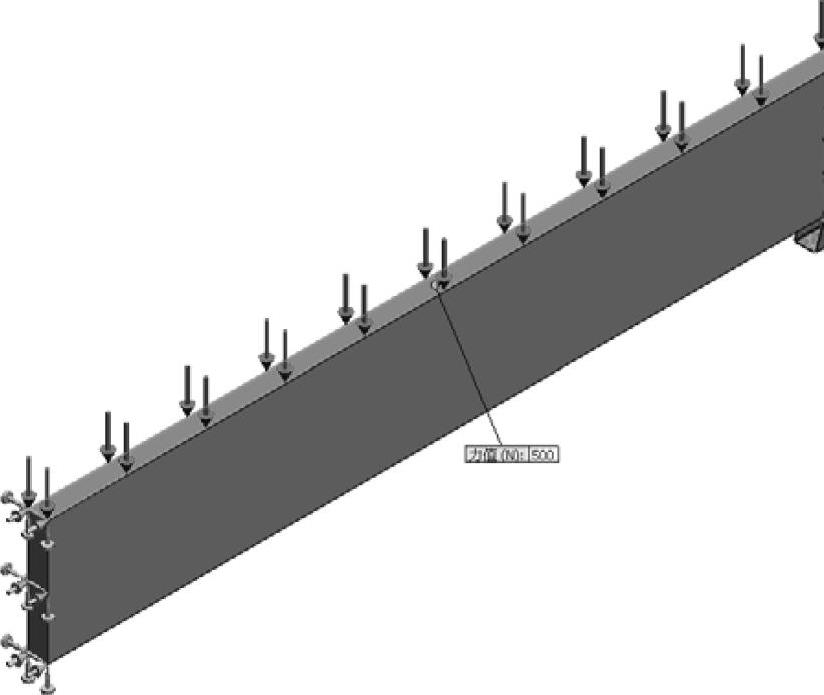
图7-44 添加外部载荷

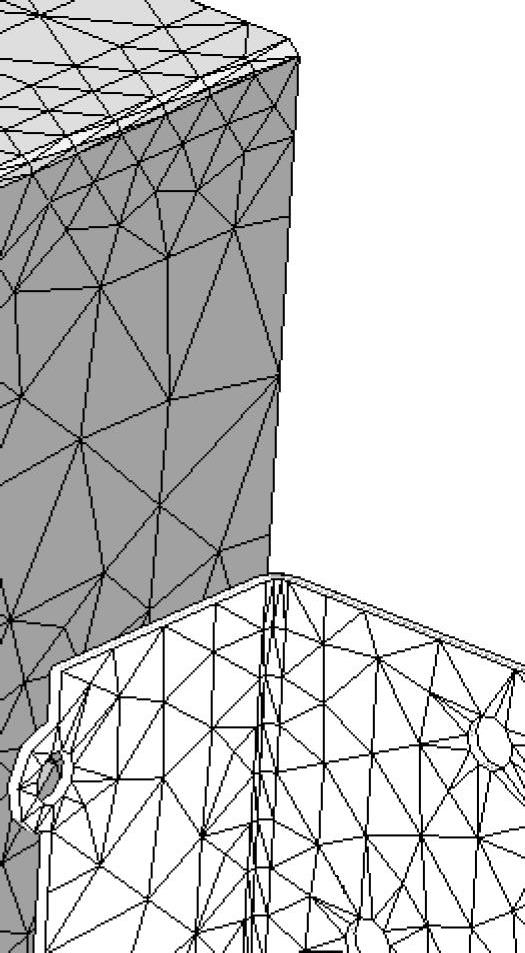
图7-45 网格划分后的结果

在【高级】下方勾选【3D渲染抽壳厚度（更慢）】复选框。横梁将会采用实体单元生成网格，而吊件会划分为壳单元，因为吊件是钣金零件。

提示

注意，这里没有必要在SolidWorks中生成曲面模型，钣金零件会被自动划分为壳单元。

步骤11 运行分析

运行这个算例，指定解算器为Direct Sparse。

提示

因为在这个算例中定义了零部件接触，且接触区域是通过几次接触迭代找到的，所以推荐使用Direct Sparse解算器。

步骤12 图解显示结果

可以观察到的最大应力为167.3MPa，低于搁栅材料的屈服强度（204MPa）。然而要想正确理解应力分布，必须单独分析joist零件，如图7-46所示。

步骤13 显示支撑件上的应力

编辑应力图解，在【高级选项】下方选择【仅显示选定实体上的图解】。设置过滤器为【选择图解的实体】并选择支撑件，如图7-47所示。

图7-46 von Mises应力分布

更改图表上限后的von Mises应力分布，如图7-48所示。可以看到四个支撑开口都显示为屈服状态。在第2章中学到，这些数值有点不切实际，在划分更细的网格后屈服也可以被忽略。

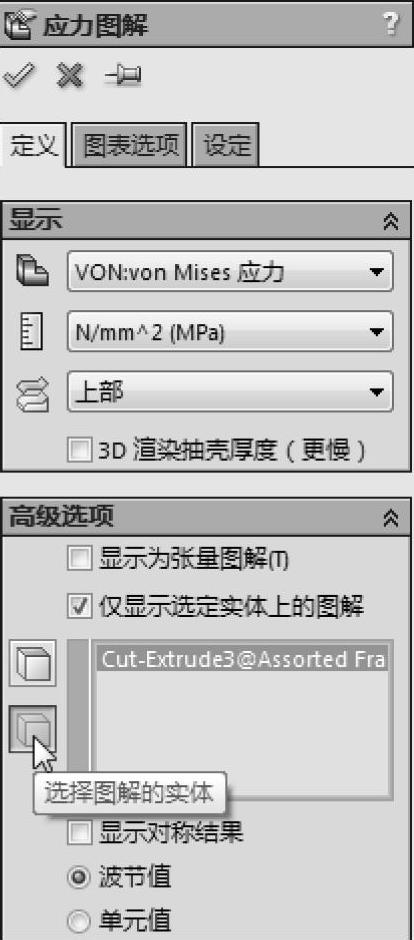
图7-47 编辑应力图解

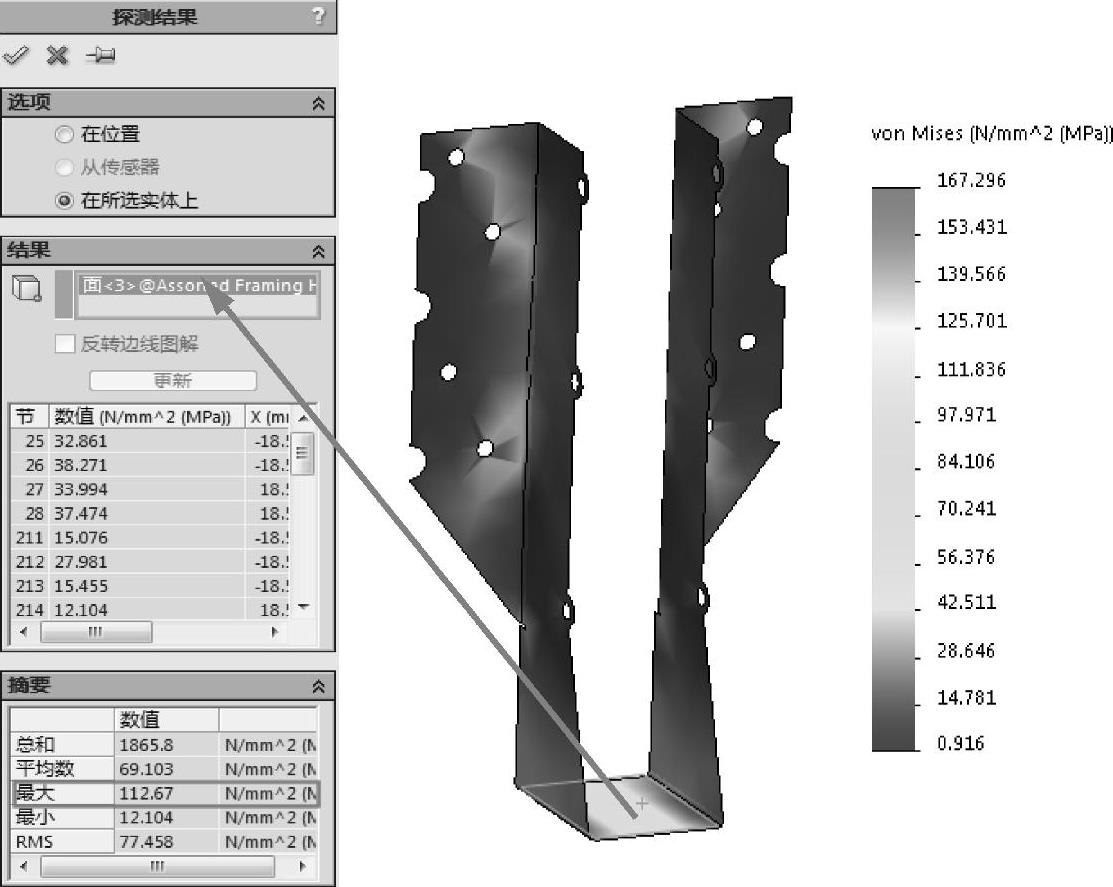
图7-48 更改图表上限后的von Mises应力分布

用户比较关注载荷承载平面的高应力，然而它的值（112.67MPa）仍然是低于屈服强度的。同时，应用钉子（这个分析中并没有采用）会有助于使载荷分布更加均匀，因此也会降低一点应力。

提示

因为选择的是一个钣金，所以外壳的两面都可以选择。

步骤14 保存并关闭文件