SolidWorks®Simulation实体网格点焊教程

如图5-73所示，一圆管由两片镀锌钢通过点焊连接两边而成。

使用FEA来计算装配体的抗扭刚度，通过扭曲该管来寻找必要的扭矩。

扭曲角度1°是随意设定的。我们并非试图重复任何实际的测试条件，只是想通过这些数字结果来比较不同的点焊结构。这两片设计是测试的第一种配置。

本练习将应用以下技术：

● 点焊。

1.项目描述 一圆管由两片厚1mm的镀锌钢制成。这两片是通过每边10处点焊连接的。焊点之间的间隙为25.4mm，每个焊点的直径为3.175mm。

通过扭曲该管1°来寻找必要的扭矩。

图5-73 圆管模型（练习5-4）

操作步骤

步骤1 打开装配体

打开文件夹“SolidWorks Simulation\Lesson05\Exercises\Spot Welds-Solid Mesk”下的装配体模型“tube solid”，并检查配置“complete tube”和“half tube”。装配体包含两个相同的零件“tube 30”。

注意，零件“tube 30”的分割线定位在焊点位置，如图5-74所示。

步骤2 装配体配置

激活配置“complete tube”。

步骤3 设定SolidWorks Simulation选项

设定全局系统单位为【公制（I）（MKS）】，【长度】单位为毫米，【应力】单位为N/m²。

步骤4 创建算例

创建名为“tube solid”的静应力分析算例。

步骤5 查看材料属性

确认材料定义（【Galvanized Steel】）已经从Solid_- Works中转移到SolidWorks Simulation。

步骤6 视圆管为实体

展开【零件】文件夹。右键单击“tube”特征并选择【视为实体】。

图5-74 分割线示意图

步骤7 定义点焊接头

右键单击【连结】文件夹并选择【点焊】。如图5-75所示，选择【点焊第一个面】，然后在另一个零件上选择连接面作为【点焊第二个面】，之后在【点焊位置】中选择如图5-75所示的10个顶点。

在【点焊直径】栏中输入【3.175mm】（0.125in）。通过这种方式，在一个侧面上所有点焊位置都被定义在同一个约束中。最后单击【确定】。

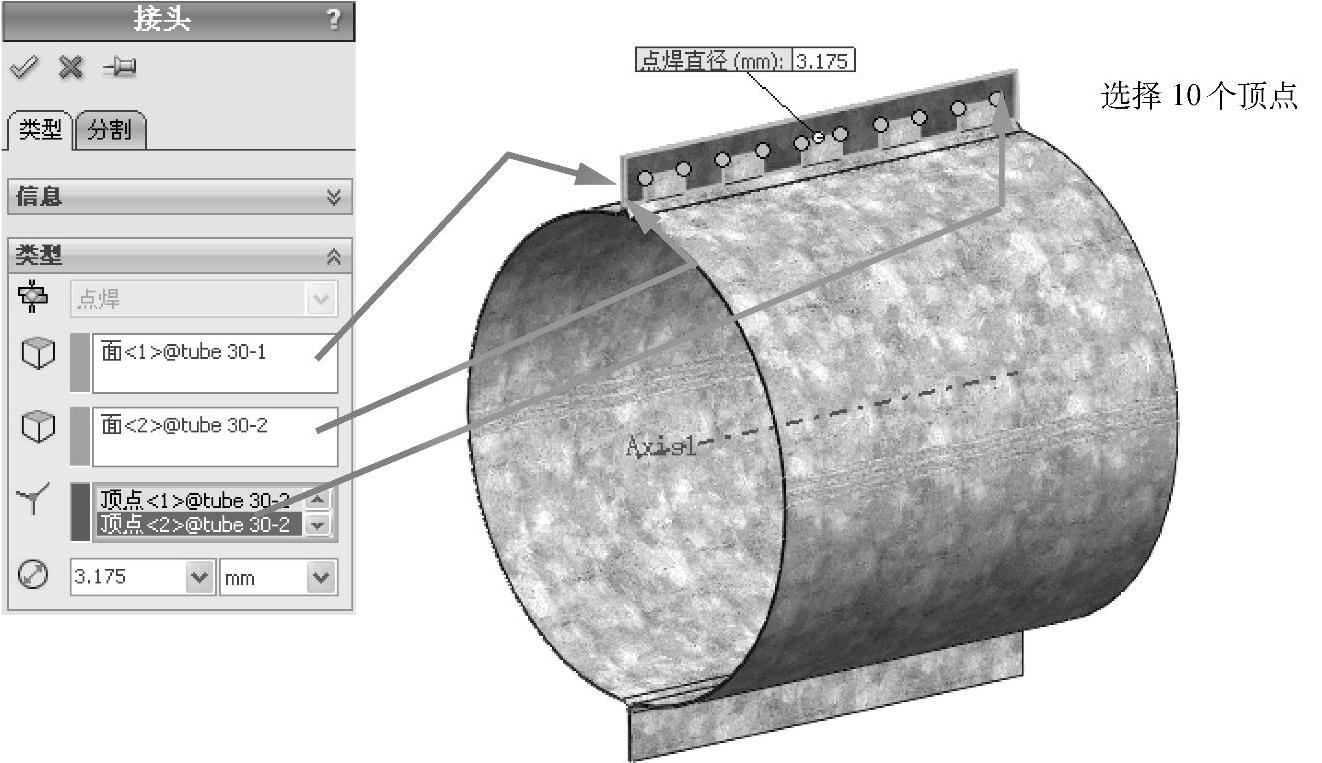
图5-75 定义点焊接头

步骤8 在圆管另外一边重复相同过程

类似地，在圆管另一侧的10个位置应用点焊，如图5-76所示。

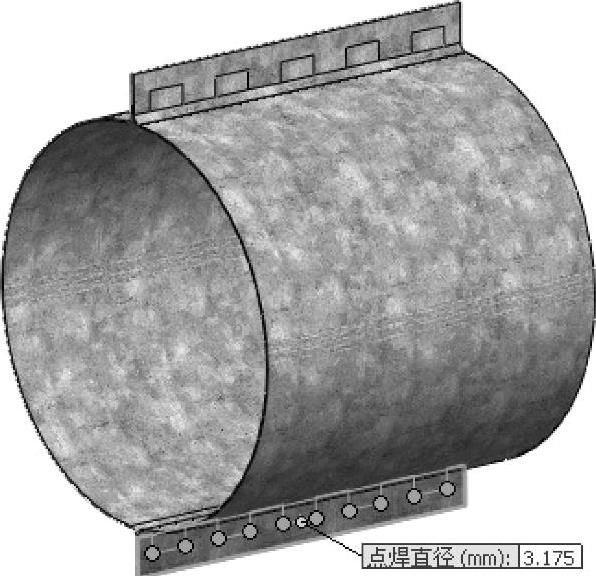
图5-76 重复定义另一侧的点焊接头

2.应用扭矩 使用两个夹具对该装配体应用扭矩。模型一端的几何体被限制了不能在轴向和圆周方向移动。在另一端，将应用1°的固定位移。

步骤9 应用夹具

选择【使用参考几何体】的高级夹具，并选择装配轴作为参考几何体。在这种方法中，约束方向与沿装配轴定义的圆柱坐标系对齐。分量一是径向位移，分量二是圆周旋转（由度数来表达），分量三是轴向位移。

在圆管的一侧选择两个面并约束【圆周】位移分量（输入【0】弧度），如图5-77所示。单击【确定】。

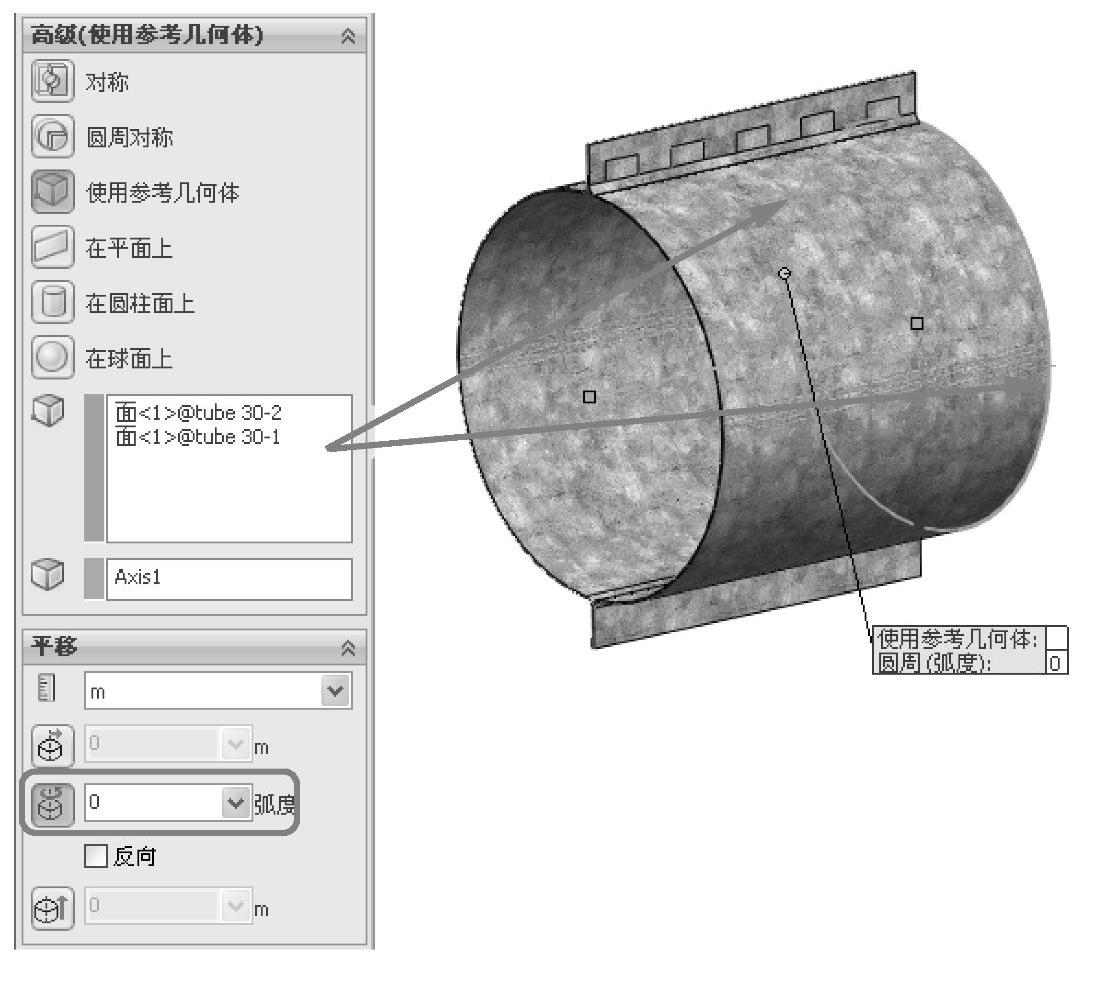
图5-77 应用夹具

步骤10 在另一端指定旋转

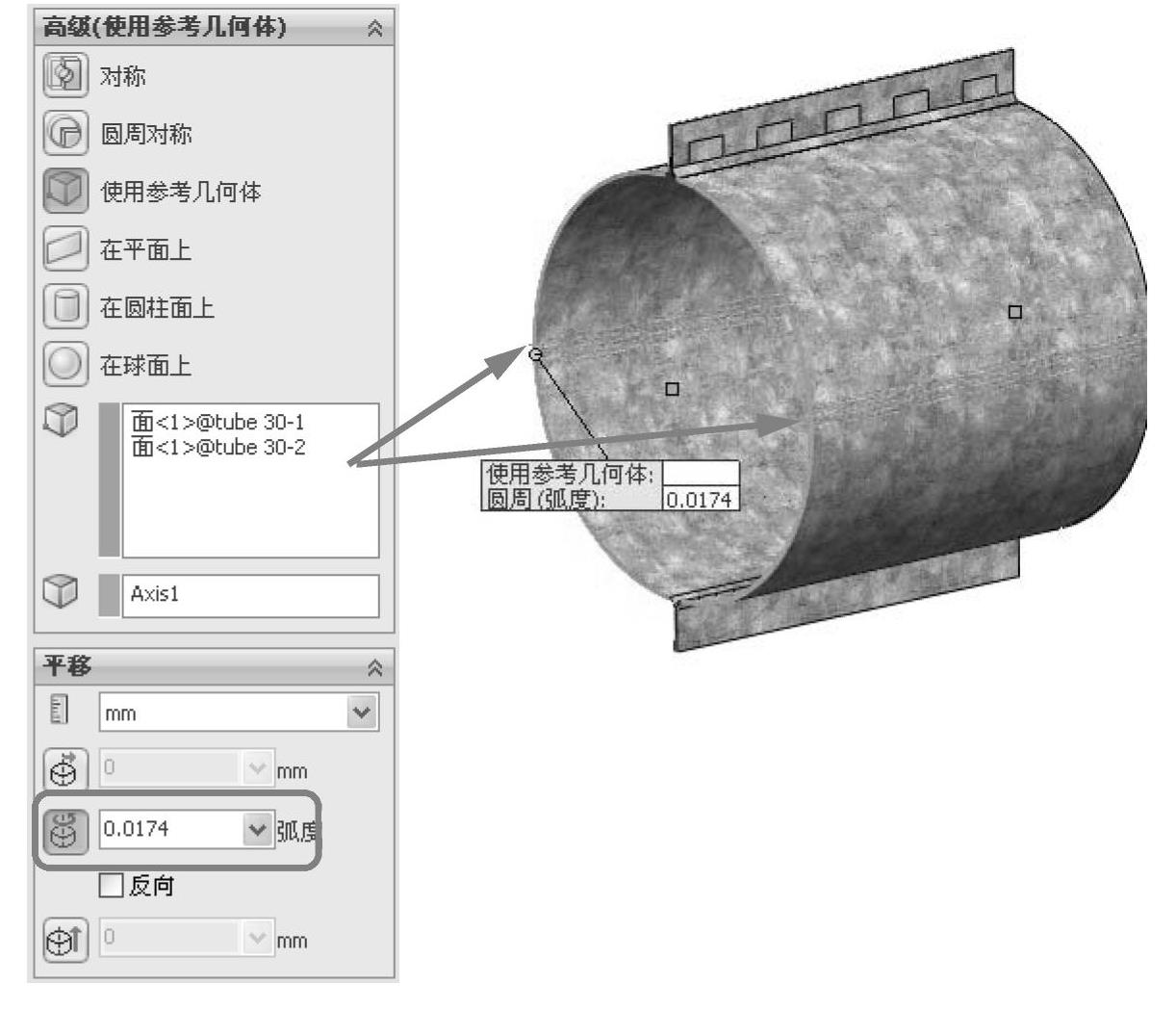
和前一条件类似，添加1°（输入【0.0174】弧度）的【圆周】位移到圆管另一端的两个面上，如图5-78所示。

(www.xing528.com)

图5-78 指定圆管另一端的旋转角度

步骤11 使用软弹簧使模型稳定

注意，在圆管两端定义的位移并没有约束装配体在轴向的位移。模型可以没有形变地在轴向移动。为了稳定该模型，勾选【使用软弹簧使模型稳定】复选框，如图5-79所示。

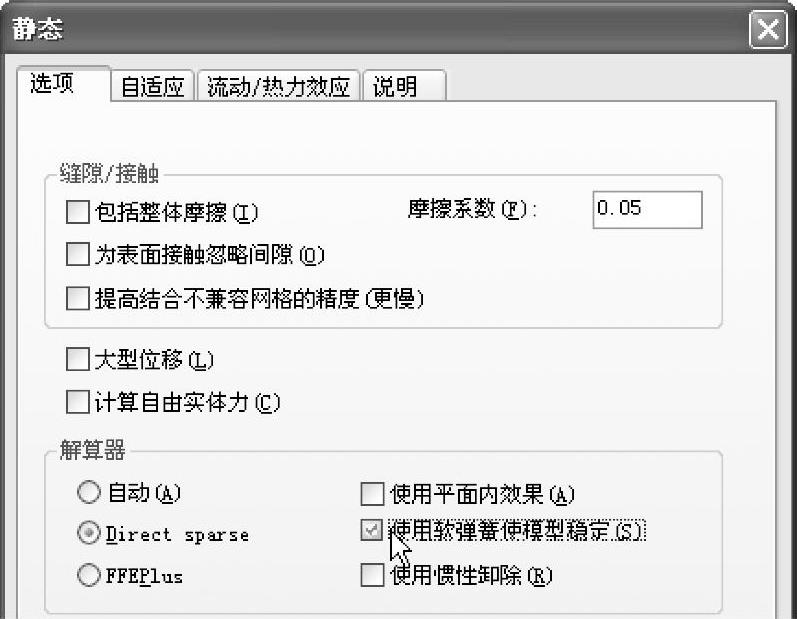
图5-79 指定算例属性选项

3.两个零件之间的接触 在对模型进行网格划分前，必须做出重要的建模决定，即两个零件是如何接触的。假设圆管的两半只是通过点焊连接，而不是通过整个相触平面连接。

假定除了指定的点焊外没有其他的交互作用，因为不需要求解接触条件，就可以方便地简化模型。然而，在点焊中细小的焊点会经常“脱落”，这是合理的假定考虑。

基于这个假定，定义两个部分接触面的接触条件为【允许贯穿】。

步骤12 定义接触

定义一个新的零部件接触类型为【允许贯穿】。

提示

顶层装配体零部件接触（全局接触）不能设置为【允许贯穿】类型。

步骤13 应用网格控制

为避免过多的单元拐角，对所有的4个圆角和凸缘应用网格控制，保持【单元大小】为3mm，【比率】为1.5，如图5-80所示。

图5-80 应用网格控制的位置

4.单元拐角 45°拐角意味着一个单元面“缠绕”包覆45°弧。通常讲，一个单元拐角为45°或者更小是首选的。

图5-81显示了有无局部网格控制的网格划分结果。

5.点焊——应力集中 注意网格只有一个单元越过壁厚。通常，推荐使用两层二阶单元。在分析变形时可以采用一层单元，但是有可能在细节的应力结果分析中产生较高的应力错误。

采用一层单元是因为要分析的是变形而不是应力。除此以外，模拟【点焊】接头模型无论如何也不适于详细的应力分析。【点焊】接头模拟波节对波节连接，该计算结果在无限应力上接近点焊。

【点焊】模型适于变形和全局应力分析，正是该模型中我们的意图。

同时，利用壳单元比实体单元可以更好地对该几何模型进行网格划分。用户使用实体单元来试验由实体几何体建立的【点焊】模型。在后面的章节，将使用壳单元来求解同样的模型。

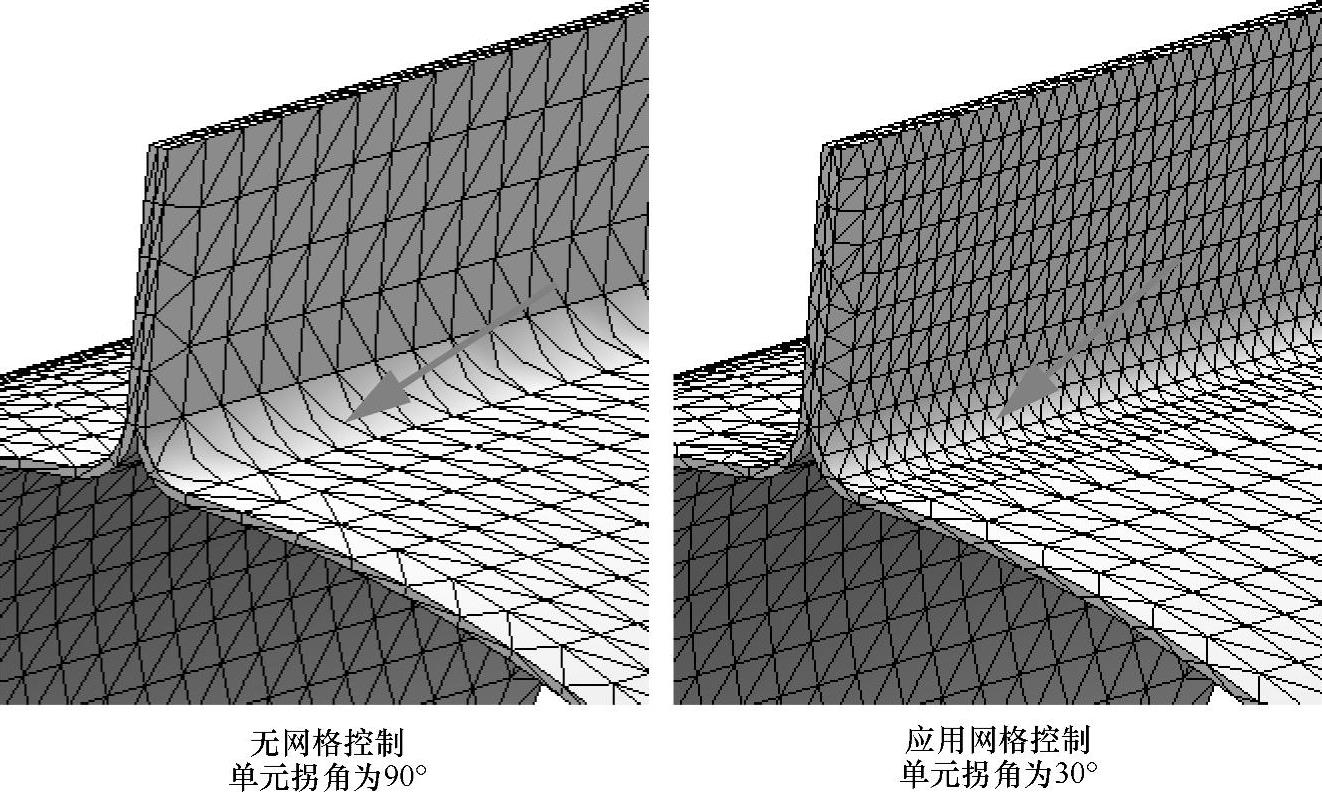
图5-81 有无局部网格控制的网格划分结果

步骤14 划分网格

在【网格参数】下选择【基于曲率的网格】。

使用【高】品质单元划分网格，并将【网格密度】的滑条移至【良好】一侧。

步骤15 运行分析

步骤16 图解显示von Mises应力

von Mises应力结果表明高应力都发生在点焊附近，如图5-82所示。正如以前所说的，任何点焊附近的应力结果都是不可靠的。

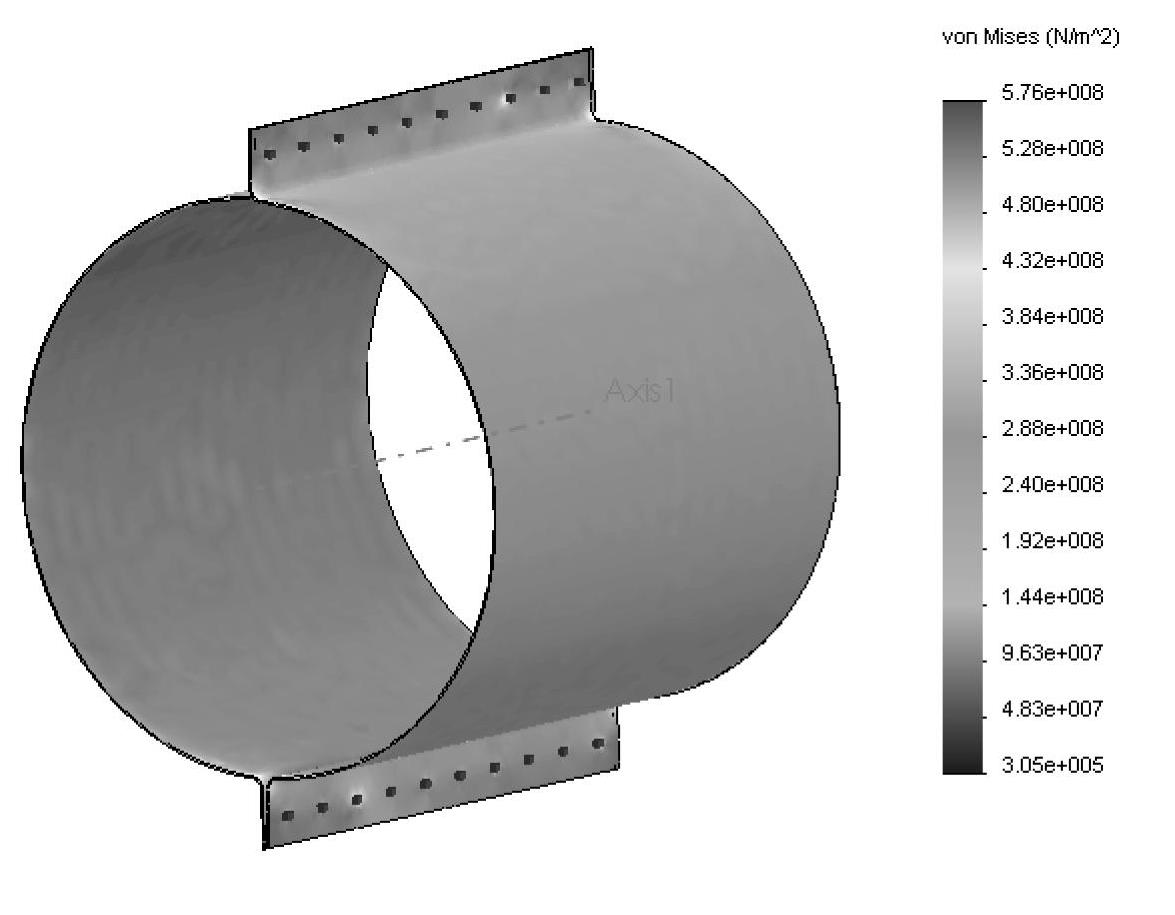
图5-82 von Mises应力分布

6.获取合力扭矩 要计算合力扭矩，首先列出圆柱坐标系下反作用力的Y方向分量，并乘以半径值。

步骤17 列举圆柱坐标系下的反作用力

列举由Axis1定义的圆柱坐标系下反作用力的Y方向分量（见图5-83）。反作用力的圆周分量为8584.9N，计算合力扭矩。

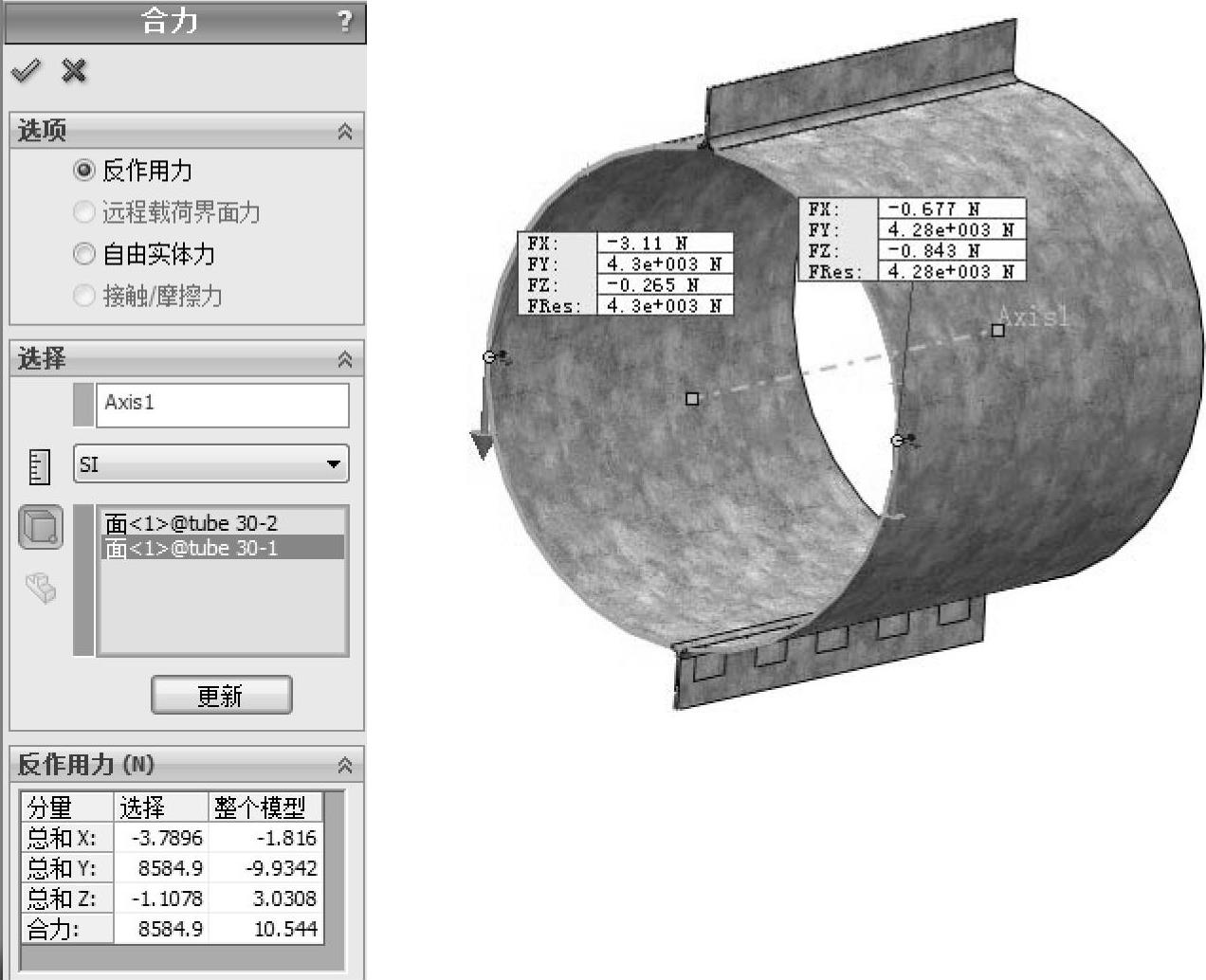
图5-83 列举圆柱坐标系下的反作用力

平均半径为0.1265m，因此合力扭矩T为

T=8584.9N×0.1265m=1085.99N·m

步骤18 保持并关闭文件

提示

第7章的练习“点焊——壳网格”中显示了如何使用壳单元分析这个问题，壳网格是一项独特的建模方法，适用于薄壳结构。