SolidWorksSimulation教程：单元类型简介

SolidWorks Simulation中有四种单元类型：一阶实体四面体单元、二阶实体四面体单元、一阶三角形壳单元和二阶三角形壳单元，下文将依次描述这些单元。

SolidWorks Simulation称一阶单元为“草稿品质”单元，二阶单元为“高品质”单元。

1.一阶实体四面体单元 一阶（草稿品质）实体四面体单元在体内沿着面和边缘模拟一阶（线性）位移场。一阶（线性）位移场命名了该单元的名称，即一阶单元。如果读者能够从材料力学中回忆起应变是位移的一阶导数，那么应变（从位移的导数中求出）和应力在一阶实体四面体单元中均为常数。

每个一阶实体四面体单元都有4个节点，分别对应四面体的4个角点。每个节点有3个自由度，意味着节点位移可完全由3个位移分量来表示。关于自由度的详细阐述将在稍后讲解。变形前后的一阶实体四面体单元如图0-3所示。

一阶单元的边是直线，面是平面。在单元加载变形后，这些边和面必须仍保持直线和平面。

由一阶单元组成的网格，其模拟出的真实复杂的位移和应力场是有严重局限性的；并且，直线和平面不能正确地模拟曲面形几何模型。

图0-4显示了一个使用一阶实体四面体单元构成的肘形几何体，显然用直线和平面模拟曲面形的几何模型是失败的。

图0-3 变形前后的一阶实体四面体单元

为了示范，我们使用了很大的（与模型尺寸相比较而言）单元来划分网格，这样的网格对任何分析来说都是不够精细的。

2.二阶实体四面体单元 二阶（高品质）实体四面体单元模拟了二阶（抛物线形）位移场以及相应的一阶应力场（注意抛物线形函数的导数是线性函数）。二阶位移场命名了该单元的名称：二阶单元。

每个二阶实体四面体单元有10个节点（4个角点和6个中间节点），并且每个节点有3个自由度。

当单元因加载而变形时，如果单元需要模拟曲线型几何模型，则二阶单元的边和面就可以是曲线形。变形前后的二阶实体四面体单元如图0-5所示。

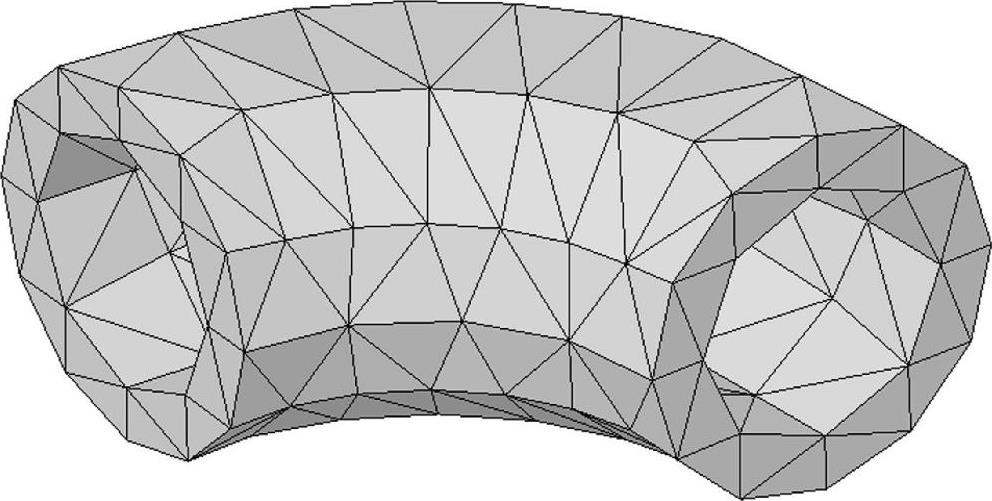
图0-4 一阶实体四面体单元网格划分结果

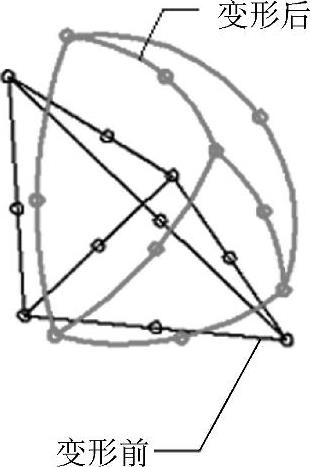
图0-5 变形前后的二阶实体四面体单元

因此，图0-6显示同样的肘形几何体，这些单元能够很好地模拟其曲线形状。

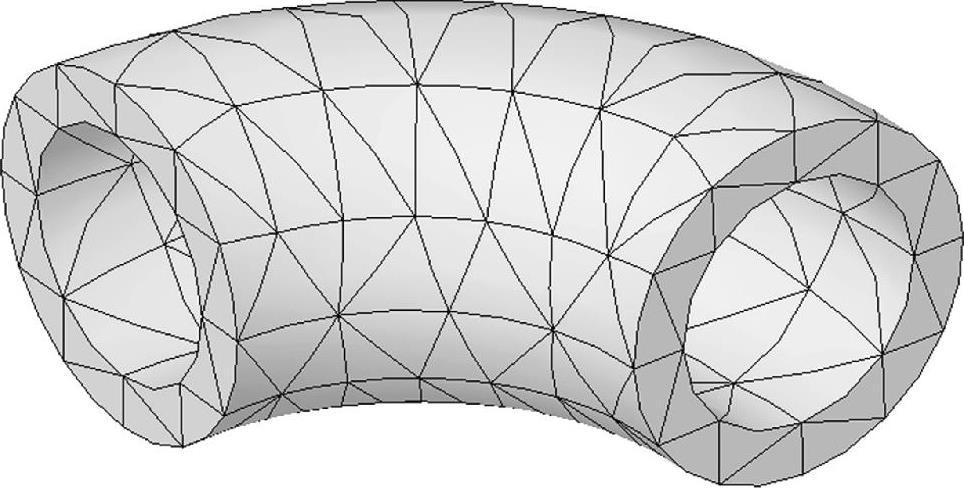
图0-6 二阶实体四面体单元网格划分结果

为了示范，我们使用很大的（与模型尺寸相比较而言）单元来划分网格。对于分析来说，即使是二阶单元，这些网格也是不够精细的，尽管与一阶单元相比，它对网格的精细程度要求较低。

为了获得精确的应力结果，建议大家在沿壁厚方向使用两层的二阶单元。

由于二阶实体四面体单元具有较好的绘图能力和模拟二阶位移场的能力，在大多数情况下Solid-Works Simulation采用它进行分析，即使它比一阶单元需要更多的计算量。(www.xing528.com)

3.一阶三角形壳单元 类似于一阶实体单元，一阶三角形壳单元沿其面和边模拟线性位移场，以及常数应变和应力。当单元变形时，一阶壳单元的直边仍保持为直线。

每个一阶壳单元有3个节点（分布在角点上），并且每个节点有6个自由度，这意味着它的位移可完全由3个平移分量和3个转动分量描述。变形前后的一阶三角形壳单元如图0-7所示。

如果用中面代表肘形几何体，并将该面用一阶壳单元进行网格划分，注意到曲面形几何体仍然不够精确。

这个结果类似于之前用一阶单元模拟曲面形几何体的不精确的结果，如图0-8所示。

与一阶实体单元相似，这些壳单元对于真实的分析来说太大了。在图0-8中，不同的颜色用来表示单元的顶面（棕色）和底面（绿色）。方向和颜色是任意的，可以通过“反向”加以改变。在任何情况下，它们都不代表模型的方向或几何体。

4.二阶三角形壳单元 二阶（高品质）三角形壳单元模拟二阶位移场和一阶（线性）应力场。

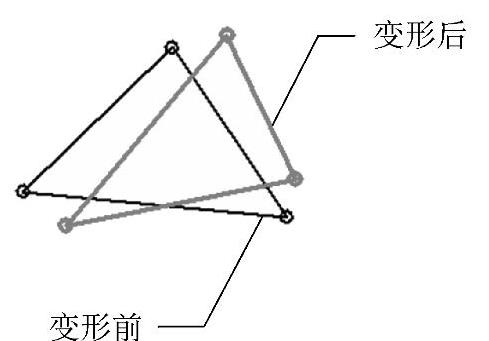
图0-7 变形前后的一阶三角形壳单元

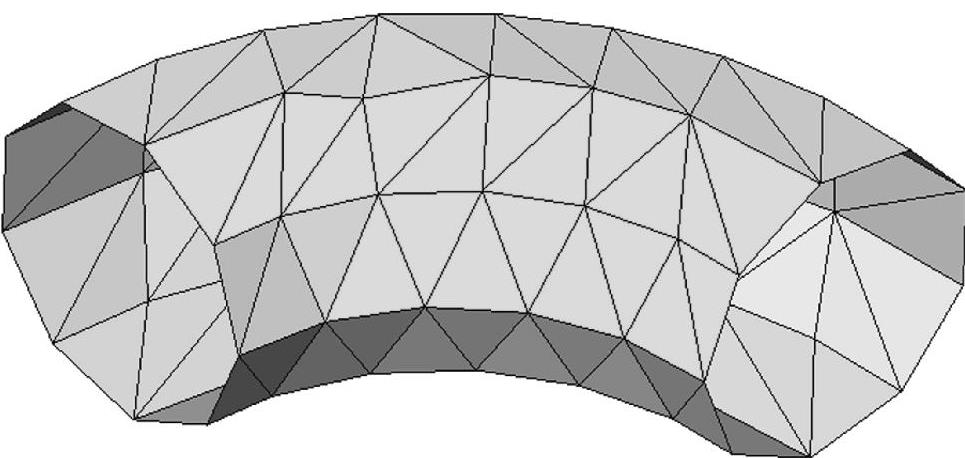
图0-8 一阶三角形壳单元网格划分结果

每个二阶壳单元有6个节点：3个角点和3个中间节点。在划分网格过程中，当单元因加载而变形时，如果需要模拟曲线形几何模型，二阶壳单元的边和面就可以模拟曲线形状。变形前后的二阶三角形壳单元如图0-9所示。

再次应用肘形体，可见这个使用二阶壳单元划分的网格精确地重现了曲线形的几何体，如图0-10所示。

图0-9 变形前后的二阶三角形壳单元

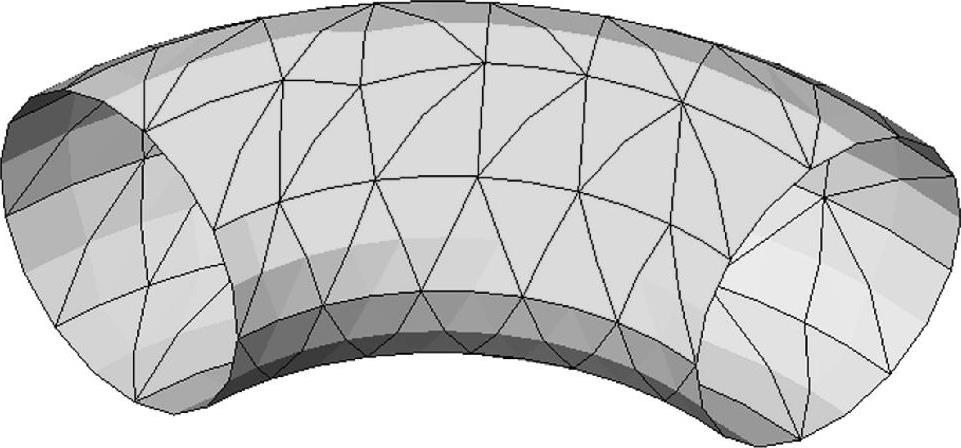
图0-10 二阶三角形壳单元网格划分结果

为了示范，我们使用很大的（与模型尺寸相比较而言）单元来划分网格。对于分析来说，即使是二阶单元，这些网格也是不够精细的，尽管与一阶单元相比，它对网格的精细程度要求较低。

5.横梁单元 相对于一阶实体和壳单元，两个节点的梁单元把两个面外挠度模拟为三次函数，并把轴向平移和扭转模拟为线性。两节点梁单元的形状在初始时为平直的，但可以假定形状在变形发生后为三次方的一个函数。

两节点的梁单元在每个端节点处都有6个自由度：3个平移自由度和3个旋转自由度。横梁单元变形前后如图0-11所示。

图0-11 横梁单元变形前后

两节点梁单元的网格映射机制与一阶实体和壳单元中的方法是相同的。