前面用最小二乘法给出了回归系数的最小二乘估计,并由此给出了回归方程.但回归方程并没有事先假定 与x一定存在线性关系.对于变量x与Y的任意一组观测数据(x i,y i),i=1,2,…,n,都可以求出一条回归直线方程
与x一定存在线性关系.对于变量x与Y的任意一组观测数据(x i,y i),i=1,2,…,n,都可以求出一条回归直线方程 =^a+^bx,但这两个变量之间是否真的存在线性关系?如果数学模型Y=a+bx+ε中b=0,说明x对Y没有影响,自然Y与x之间没有线性关系,这样其回归直线方程就没有意义了;如果b≠0,则说明Y与x之间存在线性关系.因此,首先提出待检验的原假设H 0:b=0.
=^a+^bx,但这两个变量之间是否真的存在线性关系?如果数学模型Y=a+bx+ε中b=0,说明x对Y没有影响,自然Y与x之间没有线性关系,这样其回归直线方程就没有意义了;如果b≠0,则说明Y与x之间存在线性关系.因此,首先提出待检验的原假设H 0:b=0.
关于检验H 0的方法,常用的有F检验法,t检验法和相关系数检验法,以下分别介绍.
9.1.3.1 F检验法
为了寻找检验H 0的方法,将x对Y的线性影响与随机波动引起的变差分开.记![]() ,称它为观察值y 1,y 2,…,y n的离差平方和.
,称它为观察值y 1,y 2,…,y n的离差平方和.
![]() 反映了观察值y i(i=1,2,…,n)总的分散程度,对
反映了观察值y i(i=1,2,…,n)总的分散程度,对![]() 进行分解,得到
进行分解,得到

式中,![]() .可以证明,上式最后一项等于零,由此得
.可以证明,上式最后一项等于零,由此得

式中,

![]() 叫做回归平方和,由于
叫做回归平方和,由于![]() ,所以
,所以![]() 是回归值
是回归值![]() 的离差平方和,它反映了
的离差平方和,它反映了![]() 的分散程度,这种分散程度是由于Y与x之间线性关系引起的.
的分散程度,这种分散程度是由于Y与x之间线性关系引起的.![]() 叫做残差平方和,它反映了y i与回归值
叫做残差平方和,它反映了y i与回归值![]() 的偏离程度,它是x对Y的线性影响之外的其余因素产生的误差.
的偏离程度,它是x对Y的线性影响之外的其余因素产生的误差.
回归平方和![]() 占离差平方和
占离差平方和![]() 的比例称为判定系数(coefficient of determination),也称决定系数,记作R 2,其计算公式为
的比例称为判定系数(coefficient of determination),也称决定系数,记作R 2,其计算公式为

判定系数(或决定系数)R 2可以用于检验回归直线对数据的拟合程度.如果所有观测点都落在回归直线上,则残差平方和![]() 0,此时
0,此时![]() ,于是R 2=1,拟合是完全的;如
,于是R 2=1,拟合是完全的;如![]() ,则R 2=0.可见R 2∈[0,1].R 2越接近1,回归直线的拟合程度越好;R 2越接近0,回归直线的拟合程度越差.
,则R 2=0.可见R 2∈[0,1].R 2越接近1,回归直线的拟合程度越好;R 2越接近0,回归直线的拟合程度越差.
可以证明,在H 0成立时,有统计量

如果Y与x之间线性关系显著,则![]() 的值较大,因而F的值也较大;反之,如果Y与x之间线性关系不显著,则
的值较大,因而F的值也较大;反之,如果Y与x之间线性关系不显著,则![]() 的值较小,因而F的值也较小.所以,我们可以根据F值的大小来检验H 0是否成立.
的值较小,因而F的值也较小.所以,我们可以根据F值的大小来检验H 0是否成立.
对于给定的显著性水平α,拒绝域为W={F>Fα(1,n-2)}.即,如果F>Fα(1,n-2),则拒绝H 0,即可以认为Y与x之间线性关系显著;反之,则不能拒绝H 0,即可以认为Y与x之间不存在线性关系,或线性回归方程无意义.
在计算F的值时,常用到下列公式,
例9.1.3 在硝酸钠的溶解试验中,测得在不同温度x下,溶解于100份水中的硝酸钠的份数y的数据见表9-3,(1)求y关于x的线性回归方程;(2)在显著性水平α=0.05下,检验(1)中回归方程的显著性.
表9-3 试验数据

解 (1)现在n=9,为了求线性回归方程,所需计算列在表9-4中.
表9-4 有关计算

根据表9-4,得L xx=4060,L xy=3535.3,(https://www.xing528.com)

于是,得到回归直线方程
![]()
(2)对于给定的显著性水平α=0.05,提出假设H 0:b=0.
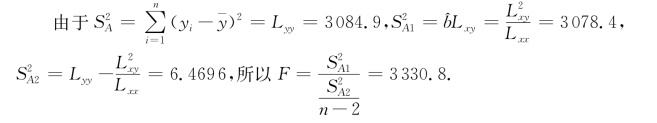
对于给定的显著性水平α=0.05,查F分布表得Fα(1,n-2)=F 0.05(1,7)=5.59,所以F=3330.8>5.59=Fα(1,n-2),则拒绝H 0,即在显著性水平α=0.05下,可以认为线性回归方程有显著意义.
9.1.3.2 t检验法
可以证明

对于给定的显著性水平α,拒绝域为![]() .即,如果|t|>
.即,如果|t|>![]() ,则拒绝H 0,可以认为Y与x之间线性关系显著;反之,则不能拒绝H 0,即可以认为Y与x之间不存在线性关系,或线性回归方程无意义.
,则拒绝H 0,可以认为Y与x之间线性关系显著;反之,则不能拒绝H 0,即可以认为Y与x之间不存在线性关系,或线性回归方程无意义.
根据例6.2.4,若t~t(n),则t 2~F(1,n),所以F检验法和t检验法在本质上是相同的.
例9.1.4 某职工医院用光电比色计检验尿汞时,得尿汞含量x mg/L与消化系统读数y的结果见表9-5.
表9-5 尿汞数据

假定Y与x服从一元线性回归模型.(1)建立y对x的回归方程,并计算σ2的估计值;(2)在显著性水平α=0.05下,检验y与x是否存在显著线性关系.
解 根据表9-5,所需计算列表见表9-6.
表9-6 有关计算

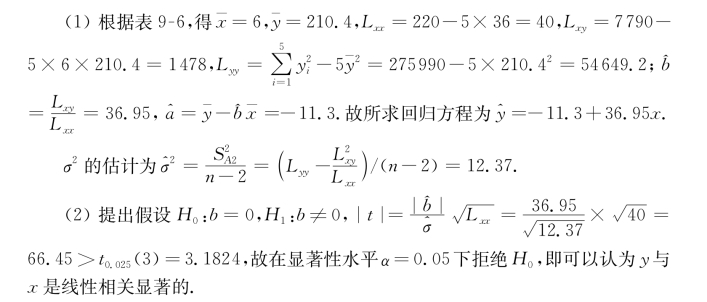
9.1.3.3 相关系数检验法
根据第4章知,相关系数的大小可以表示两个随机变量线性关系的密切程度.对于线性回归中的变量x与Y,其样本的相关系数为

给定显著性水平α,查相关系数表(见书末附录C的附表6)得rα(n-2),根据试验数据(x i,yi)(i=1,2,…,n)计算r的值,当|r|>rα(n-2)时,则拒绝H 0,即可以认为Y与x之间线性关系显著;反之,当|r|≤rα(n-2)时,则不能拒绝H 0,即可以认为Y与x之间不存在线性关系,或线性回归方程无意义.
可以证明F检验法和相关系数检验法本质上是相同的(证明从略),因此,F检验法,t检验法和相关系数检验法本质上都是相同的.
例9.1.5 在例9.1.3中,由于L xx=4060,L xy=3535.3,L yy=3537.4,则r .查相关系数表得rα(n-2)=r 0.05(7)=0.6664<0.932738=|r|,因此在显著性水平α=0.05时,拒绝H 0,即可以认为y与x是线性相关显著的(这个结果与例9.1.3相同).在例9.1.4中,由于L xx=40,L xy=1478,L yy=54649.2,则
.查相关系数表得rα(n-2)=r 0.05(7)=0.6664<0.932738=|r|,因此在显著性水平α=0.05时,拒绝H 0,即可以认为y与x是线性相关显著的(这个结果与例9.1.3相同).在例9.1.4中,由于L xx=40,L xy=1478,L yy=54649.2,则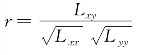
 查相关系数表得rα(n-2)=r 0.05(3)=0.8783<0.99966=|r|,因此在显著性水平α=0.05时,拒绝H 0,即可以认为y与x是线性相关显著的(这个结果与例9.1.4相同).
查相关系数表得rα(n-2)=r 0.05(3)=0.8783<0.99966=|r|,因此在显著性水平α=0.05时,拒绝H 0,即可以认为y与x是线性相关显著的(这个结果与例9.1.4相同).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




