《概率论与数理统计》中的回归系数最小二乘估计

如果μ（x）＝a＋bx，此时估计μ（x）的问题称为一元线性回归问题．假设对于x的每一个值，有Y～N（a＋bx，σ2），其中a，b，σ2都是不依赖于x的未知参数．记ε＝Y-（a＋bx），这相当于

式中，a，b，σ2都是不依赖于x的未知参数．称式（9．1．1）为一元线性回归模型，b称为回归系数．

以下给出a，b的估计．取x的n个不完全相同的值x 1，x 2，…，x n，做独立试验，得到样本（x 1，Y 1），（x 2，Y 2），…，（x n，Y n）．根据式（9．1．1），知道Y i＝a＋bx i＋εi，εi～N（0，σ2），各εi相互独立．

由于Y i～N（a＋bx i，σ2），i＝1，2，…，n，且Y 1，Y 2，…，Y n相互独立，故而Y 1，Y 2，…，Y n的联合密度函数为

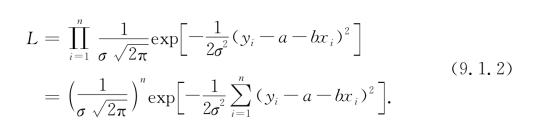
以下应用极大似然估计法给出a，b的估计．要使似然函数L取最大值，只要式（9．1．2）的右边括弧中的平方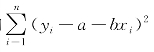部分为最小，即

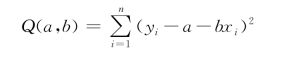
取最小值．

以下根据最小二乘原理来确定a，b，使Q（a，b）取最小值，这样得到的估计称为最小二乘估计．分别求Q关于a，b的偏导数，并令它们为零，即

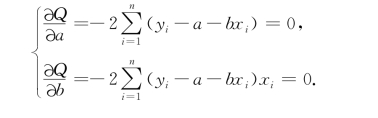
得方程组

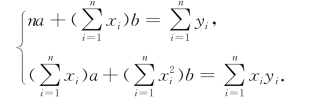
由于x 1，x 2，…，x n不完全相同，此方程组的系数行列式

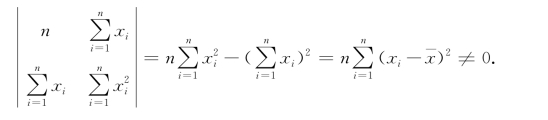
解得b和a的最小二乘估计值为

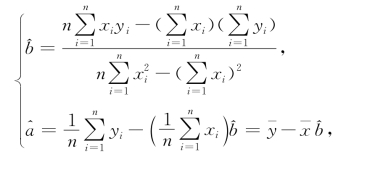(www.xing528.com)

式中，

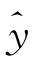在得到a和b的估计值后，对于给定的x，我们就取作为回归函数μ（x）＝a＋bx的估计，即，称为Y关于x的经验回归函数．记＝，称为Y关于x的经验回归方程，简称回归方程，其图形称为回归直线．

为了以后计算方便，我们引入下述记号

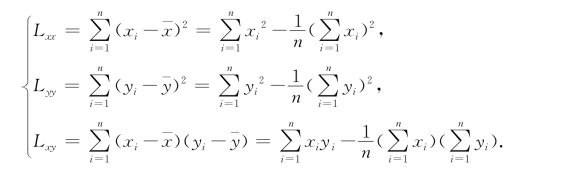
这样，b和a的最小二乘估计值可以写成

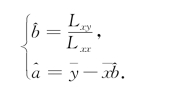
例9．1．2（续例9．1．1）设在例9．1．1中的随机变量Y符合式（9．1．1）所述的条件，求Y关于x的线性回归方程．

解　现在n＝10，为了求线性回归方程，所需计算列在表9-2中．

表9-2　有关计算

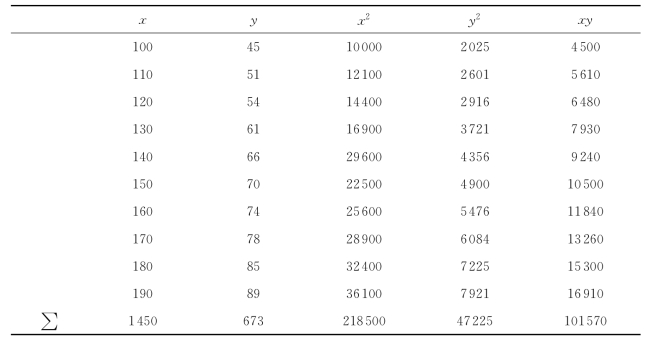
根据表9-2得

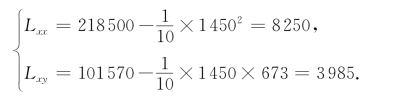
因此，b和a的最小二乘估计值为

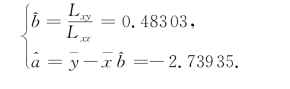
于是，得到线性回归方程