在许多实际问题中，变量之间存在着相互依存的关系．一般地，变量之间的关系可以大体上分为两类，一类是确定性关系，即存在确定的函数关系，如圆的面积S与半径r之间的关系为S＝πr 2；另一类是非确定性关系，即它们之间有密切关系，但又不能用函数关系式来精确表示，如人的身高与体重的关系，炼钢时钢的含碳量与冶炼时间的关系．有时即使两个变量之间存在数学上的函数关系，但由于实际问题中的随机因素的影响，变量之间的关系也经常有某种不确定性．变量之间的这种不确定性关系，称为相关关系．分析变量之间的相关关系的方法，称为相关分析．
一般地，由一个或一组非随机变量来估计或预测某一个随机变量的观测值时，所建立的数学模型及所进行的统计分析，称为回归分析（regression analysis）．如果这个数学模型是线性的，就称为线性回归分析．
设有两个变量x和Y，其中x是可以精确测量或控制的非随机变量，而Y是随机变量．x的变化引起Y的变化，但它们之间的变化又不是确定的．例如，人的身高是可以精确测量的，但对某一确定身高的人，其体重是一个随机变量，它们之间有一定的关系，但不是确定的．如果x取任意一个值时，Y相应地服从某一个分布，则变量x与随机变量Y之间存在相关关系．如果我们处理的是两个变量之间的相关关系，而这种关系又是线性的，这种回归分析就称为一元线性回归分析．
我们对于x取一组不完全相同的值x 1，x 2，…，x n，设Y 1，Y 2，…，Y n分别是在x 1，x 2，…，x n处对Y的独立观察结果，称（x 1，Y 1），（x 2，Y 2），…，（x n，Y n）是一个样本，对应的样本观察值记为（x 1，y 1），（x 2，y 2），…，（x n，y n）．
我们首先要解决的问题是如何利用样本来估计Y关于x的回归函数E（Y）＝μ（x）．为此，首先需要推测μ（x）的形式．可以根据观察值（x i，y i）在直角坐标系中描出它的相应的点（图9-1），这种图称为散点图（scatter diagram）．散点图可以帮助我们粗略地看出μ（x）的形式．
例9．1．1 为研究某一个化学反应过程温度x对产品的得率Y（%）的影响，测得数据见表9-1．
表9-1 试验数据
这里自变量x是普通变量，Y是随机变量．根据表9-1的数据画出的散点图，如图9-1所示．从图9-1大致可以看出μ（x）具有线性函数a＋bx的形式．(www.xing528.com)
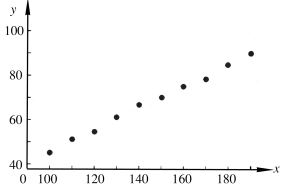
图9-1 散点图
回归分析的基本思想和方法以及“回归”名词的由来，要归功于英国统计学家高尔顿．高尔顿和他的学生、现代统计学的奠基者之一皮尔逊在研究父母身高与其子女身高的遗传关系时，观察了1078对夫妇，以每对夫妇的平均身高作为x，而取他们的一个成年儿子的身高作为y，将这些数据画成散点图，发现趋势近似一条直线
＝33．73＋0．516x（单位：in，1in＝2．54cm）．这表明：
（1）父母平均身高x每增加1个单位时，其成年儿子的身高y也平均增加0．516个单位．
（2）一群高个子父辈的儿子们的平均身高要低于他们父辈的平均身高．比如，x＝80，那么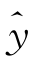
＝75．01．
（3）低个子父辈的儿子们虽然仍为低个子，但是平均身高却比他们的父辈增加一些．比如，x＝60，那么
＝64．69．
正是因为子代的身高有回归到父辈平均身高的这种趋势，才使人类的身高在一定时期内相对稳定．这个例子生动地说明了生物学中“种”的稳定性．正是为了描述这种有趣的现象，高尔顿引进了“回归”这个名词来描述父辈身高x与子代身高y的关系．尽管“回归”这个名称有特定的含义，人们在研究大量的问题中的变量x与y之间的关系并不具有这种“回归”的含义，但借用这个名词把研究变量x与y之间的关系的数学方法称为回归分析，也算是对高尔顿这个伟大的统计学家的一个纪念．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
