复习题8．2详解
1．对二项分布B（n，p）作统计假设H 0：p＝0．6，H 1：p≠0．6，检验H 0的拒绝域取为W＝｛X≤1｝∪｛X≥9｝，其中X为10次实验中成功的次数，求显著性水平α和备择假设p＝0．3时犯第二类错误的概率β．
2．如果一个矩形的宽度w与长度l的比
，这样的矩形称为黄金矩形．这种尺寸的矩形使人们看上去有良好的感觉．现代的建筑构件（如窗架）、工艺品（如图片镜框）、甚至司机的执照、商业的信用卡等常常都是采用黄金矩形．下面列出某工艺品工厂随机取的20个矩形的宽度与长度的比值：0693，0．749，0．654，0．670，0．662，0．672，0．615，0．606，0．690，0．628，0．668，0．611，0．606，0．609，0．601，0．553，0．570，0．844，0．576，0．933．设这一工厂生产的矩形的宽度与长度的比值总体服从正态分布，其均值为μ，方差为σ2，μ，σ2均未知．试检验假设（取显著性水平α＝0．05）H 0：μ＝0．618，H 1：μ≠0．618．
3．某厂生产的某种钢索的断裂强度X服从正态分布X～N（μ0，σ2），其中σ＝40kg／cm2．现从一批这种钢索中抽取容量为9的一个样本，测得断裂强度的平均值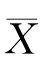
，与以往正常生产时的平均值相比，
较μ0大18．若设总体方差不变，问在显著性水平α＝0．01下，能否认为这批钢索质量有显著提高？
4．用过去的铸造方法，零件强度的标准差是1．6，为了降低成本，改变了铸造方法，测得用新方法铸造出的零件强度如下：51．9，53．0，52．7，54．1，53．2，52．3，52．5，51．1，54．7．设零件强度服从正态分布，取显著性水平α＝0．05，问改变方法后，零件强度的方差是否发生了改变？
5．2台车床生产同一种滚珠（设滚珠直径服从正态分布），从中分别抽取8个和9个产品：
甲车床 15．0，14．5，15．2，15．5，14．8，15．1，15．2，14．8；
乙车床 15．2，15．0，14．8，15．2，15．0，15．0，14．8，15．1，14．8．
比较2台车床生产的滚珠直径的方差是否有明显差异（取显著性水平α＝0．05）．(www.xing528.com)
6．将一正四面体的4面分别涂为红、绿、蓝、白4种不同的颜色，任意抛掷该四面体，直至白色的一面朝下为止，记录抛掷的次数，重复做如此试验200次，其结果见下表：
问该4面体是否均匀（显著性水平α＝0．02）？
7．电池在货架上滞留的时间不能太长，下面给出某商店随机选取的8只电池的货架滞留时间（以天计）：108，124，124，106，138，163，159，134，设数据来自正态总体N（μ，σ2），μ，σ2未知．试检验假设H 0：μ≤125，H 1：μ＞125．取显著性水平α＝0．05．
8．某市质监局接到投诉后，对某金店进行调查．现从其出售的标志18K的项链中抽取9件进行检测，检测标准为：标准值18K且标准差不得超过0．3K，检测结果如下：17．3，16．6，17．9，18．2，17．4，16．3，18．5，17．2，18．1，假设项链的含金量服从正态分布，试问检测结果能否认定金店出售的产品存在质量问题（取显著性水平α＝0．01）？
9．为比较两种燃料A与B的辛烷值，各取12个样品进行测试，分别测得其辛烷值的样本均值和样本方差分别为：
辛烷值越高，燃料质量越好．设两种燃料的辛烷值分别服从正态分布
，且两个样本相互独立．（1）在显著性水平α＝0．1下，检验假设
；（2）在显著性水平α＝0．05下，检验假设
10．对某汽车零件制造厂所生产的汽缸螺栓口径（单位：mm）进行抽样检验，测得100个数据，分组列表如下：
问螺栓口径是否服从正态分布？取显著性水平α＝0．05．
11．某种配偶的后代按体格属性分为3类，各类的数目分别是10，53，46．按照某种遗传模型其频率之比应该为p 2∶2p（1-p）∶（1-p）2，问数据与模型是否相符（取显著性水平α＝0．05）？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
