分布拟合检验结果分析

在前3节的讨论中，我们都是假设了总体服从正态分布，然后对其均值或方差提出假设，并进行检验，这些均属于参数假设检验问题．在实际问题中，怎样才能知道一个总体是否服从正态分布呢？更一般地说，怎样才能知道一个随机变量X的分布函数是某个给定的函数F（x）呢？

本节我们将根据样本X 1，X 2，…，X n（或其观察值x 1，x 2，…，x n），考虑如下假设检验问题：

H 0：X的分布函数为F（x）．

这里F（x）是已知的分布函数．

通常要用样本观察值来估计（或代替）F（x）的未知参数，例如，对于正态总体N（μ，σ2），取等．处理这类总体分布的假设检验问题的方法很多，这里我们只介绍最常用的一种方法——χ2检验法．

在实数轴上取k个分点t 1，t 2，…，tk，这k个点将（-∞，＋∞）分成k＋1个互不相交的区间（-∞，t 1），［t 1，t 2），…，［ti-1，ti），…，［tk，＋∞）．

设样本观察值x 1，x 2，…，x n中落入第i个区间的个数为v i（1≤i≤k＋1），其频率

如果H 0成立，由给定的分布函数F（x），可以计算得到X落在每个区间的概率为p i＝P｛ti-1≤t＜ti｝＝F（ti）-F（ti-1），其中1≤i≤k＋1，记t 0＝-∞，t k＋1＝＋∞．考虑统计量）

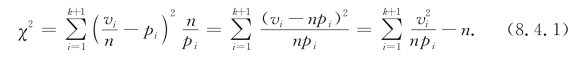
注　在式（8．4．1）中给出了统计量χ2的3种等价形式，在后面的应用中采用哪一种都可以．

式（8．4．1）中χ2依赖于vi和p i，因此它与F（x）建立了关系，它可以作为检验H 0的检验统计量．皮尔逊在1900年证明了如下定理．

定理8．4．1　设F（x）是随机变量X的分布函数，当H 0成立时，由式（8．4．1）给出的统计量χ2以χ2（k）为极限分布（当n→＋∞），其中F（x）中不含有未知参数，vi称为实际频数，np i称为理论频数．

根据定理8．4．1，当n比较大时，检验统计量χ2近似服从χ2（k）．这样，给定显著性水平α后，查χ2分布表，得临界值，使

由样本观察值x 1，x 2，…，x n计算v 1，v 2，…，vk＋1，由给定的分布函数F（x）计算p 1，p 2，…，p k＋1，从而计算出χ2的值．若，则拒绝H 0，即认为总体X的分布函数与F（x）有显著性差异；若，则不能拒绝H 0，即不能认为总体X的分布函数与F（x）有显著性差异．

需要指出的是，当F（x）中含有r个未知参数θ1，θ2，…，θr时（r＜k），则需要用估计值来分别代替θ1，θ2，…，θr，此时χ2以χ2（k-r）为极限分布（当n→＋∞）．费歇尔证明了如下定理．

定理8．4．2　设F（x）是随机变量X的分布函数，且F（x）中含有r个未知参数，当H 0成立时，由式（8．4．1）给出的统计量χ2以χ2（k-r）为极限分布（当n→＋∞）．

在定理8．4．2中，当r＝0（即F（x）中不含有未知参数）时，其结果与定理8．4．1相同．因此，定理8．4．1可以看作是定理8．4．2的一种特殊情况．

以下给出χ2检验法的一般步骤：

步骤1，在假定H 0：F（x）＝F（x；θ1，…，θr）成立的前提下，求出参数θ1，θ2，…，θr的极大似然估计

步骤2，把实数轴划分成k＋1个互不相交的区间（-∞，t 1），［t 1，t 2），…，［ti-1，ti），…，［tk，＋∞）．

步骤3，在H 0成立的前提下，计算pi和np i，其中pi为总体X的取值落入第i个区间的概率，即．

步骤4，按照样本观察值x 1，x 2，…，x n落入第i个区间内的个数（即频数）vi（i＝1，2，…，k＋1）和步骤3中计算得到的np i，计算由式（8．4．1）给出的统计量χ2的值（步骤3，步骤4中的计算可列表进行）．

步骤5，按照所给定的显著性水平α，查自由度为k-r的χ2分布表，得临界值，使，这里r为F（x）＝F（x；θ1，…，θr）中未知参数的个数．

步骤6，若，则否定H 0，即认为总体X的分布函数与F（x）有显著性差异；若，则不能否定H 0，即不能认为总体X的分布函数与F（x）有显著性差异．

由于χ2检验法是在n→＋∞时推导出来的，所以在应用时必须注意，当n比较大时，np i不能太小．在实际应用中，一般要求n不能小于50且np i不小于5．

χ2检验法对总体X是离散型和连续型分布均适用，下面举例说明．(www.xing528.com)

例8．4．1　在一批灯泡中抽取300只做寿命试验，获得的数据见表8-7．

表8-7　灯泡寿命试验数据

对于给定的显著性水平α＝0．05，问这批灯泡的寿命是否服从指数分布

解　本题是在显著性水平α＝0．05时，检验H 0：这批灯泡的寿命服从指数分布

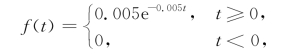
总体X的可能取值范围是［0，＋∞），把该范围分成4个互不相交的区间，如表8-7的第1行（或表8-8的第2列）．

在H 0成立时，总体X的分布函数为

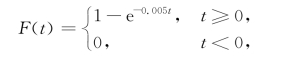
可以计算得到X落在每个区间的概率为p i＝P｛ti-1≤t＜ti｝＝F（ti）-F（ti-1）（其中i＝1，2，3，4），np i的 计算结果见表8-8．

表8-8　有关计算

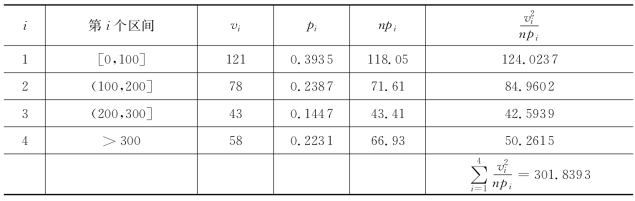
根据表8-8，得χ2＝301．8393-300＝1．8393＜7．815（3），根据定理8．4．1，在给定的显著性水平α＝0．05时不能否定H 0，即可以认为这批灯泡的寿命服从指数分布

例8．4．2　某电话站在1h内接到电话用户的呼叫次数按每分钟记录见表8-9．问在显著性水平α＝0．05时，这个分布能否看作为泊松分布？

表8-9　某电话站接到呼叫次数按每分钟记录表

解　H 0：总体X是参数为λ的泊松分布．由于λ的极大似然估计值，利用表8-9中的数据，经计算得＝2．

对于给定的显著性水平α＝0．05，根据表8-9知n＝60，k＝7，查表得临界值为＝12．592．有关计算见表8-10．

表8-10　有关计算

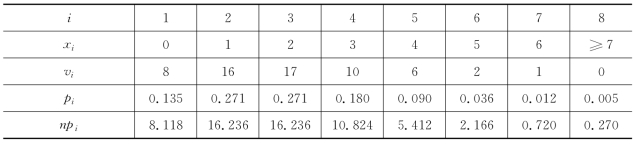
利用表8-10中的数据，得，于是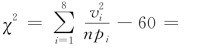0．5773＜12．592＝

根据定理8．4．2，对于给定的显著性水平α＝0．05，不能否定H 0，即可认为总体X服从参数λ＝2的泊松分布．