单个总体方差检验-概率论与数理统计（第5版）

设X 1，X 2，…，X n是来自正态总体N（μ，σ2）的样本，要求检验假设（显著性水平为α）

其中,为常数．

由于S 2为σ2的无偏估计量，当H 0为真时，S 2的观察值s 2与的比值一般在1附近摆动，而不应过分大于1或过分小于1．根据定理6．2．2知，当H 0为真时，有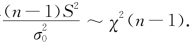取

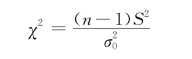
作为检验统计量，如上所述检验问题的拒绝域具有形式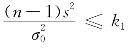或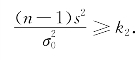这里k 1，k 2的值由下式确定：

P｛当H 0为真时拒绝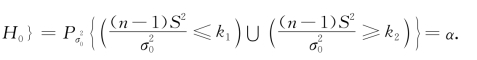

为计算方便起见，习惯上取

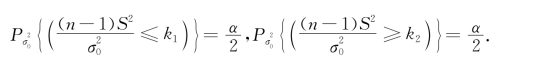
于是，因此，得拒绝域为

以下来求单边检验问题（显著性水平为α）

的拒绝域．

由于H 0中的全部σ2都要比H 1中的σ2要小，当H 1为真时，S 2的观察值s2往往偏大，因此拒绝域的形式为s2≥k．以下来确定常数k．

P｛当H 0为真时拒绝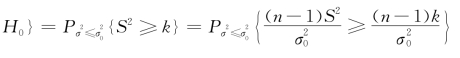

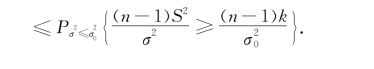
要控制P｛当H 0为真时拒绝H 0｝≤α，只需令(www.xing528.com)

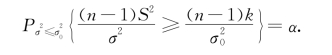
由于，根据上式，得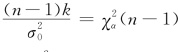．因此k＝，于是此检验问题的拒绝域为，即

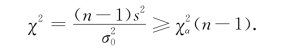
类似地，得左边检验问题

的拒绝域为

以上的检验法称为χ2检验法．

一个正态总体方差检验的拒绝域，见表8-4．

表8-4　一个正态总体方差的检验（显著性水平为α）

从表8-4的拒绝域可以看出：右边检验的拒绝域在临界点的右边，左边检验的拒绝域在临界点的左边，双边检验的拒绝域在两个临界点构成区间的外面．

例8．2．3　某工厂生产的某型号的电池，其寿命（以h计）长期以来服从方差为σ2＝5000的正态分布，现有一批这种电池，从它的生产情况来看，寿命的波动性有所改变．现随机取26个电池，测出其寿命的样本方差为s 2＝9200．根据这一数据能否推断这批电池的寿命的波动比以往的有显著性的变化（α＝0．02）？

解　本题要求在水平α＝0．02下检验假设

现在，则检验问题的拒绝域为．

由观察值s 2＝9200，得，所以在显著水平α＝0．02时拒绝H 0，即可以认为这批电池寿命的波动比以往的有显著的变化．