两类错误与假设检验的步骤

由于检验法则是根据样本作出的，总有可能作出错误的决策．在假设H 0实际为真时，可能犯拒绝H 0的错误，称这类“弃真”的错误为第一类错误．当H 0实际不真时，可能接受H 0，称这类“取伪”的错误为第二类错误．

检验的两类错误，具体情况见表8-1．

表8-1　检验的两类错误

形如式（8．1．2）中的备择假设H 1，表示μ可能大于μ0，也可能小于μ0，称为双边备择假设，而称形如式（8．1．2）的假设检验为双边假设检验．

有时，我们只关心总体均值是否增大，例如，试验新工艺以提高材料的强度．这时，所考虑的总体的均值应该越大越好．如果我们能判断在新工艺下总体均值较以往正常生产的大，则可以考虑采用新工艺．此时，我们需要检验假设：

形如式（8．1．3）的假设检验，称为右边检验．

形如式（8．1．4）的假设检验，称为左边检验．

以下来讨论单边检验（右边检验和左边检验）的拒绝域．

设总体X～N（μ，σ2），σ为已知，X 1，X 2，…，Xn是来自X的样本．给定显著性水平α，我们求检验问题H 0：μ≤μ0，H 1：μ＞μ0的拒绝域．

由于H 0中的全部μ都比H 1中的μ要小，当H 1为真时，观察值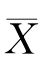往往偏大，因此，拒绝域的形式为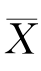≥k（k为某个正的常数）．

下面来确定常数k，其做法与例8．1．1类似．

P｛当H 0为真时拒绝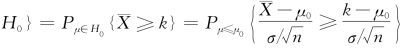

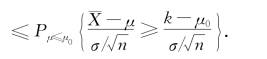
上式不等号成立是由于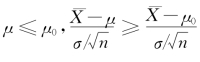，事件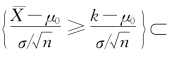要控制P｛当H 0为真时拒绝H 0｝≤α，只需令

由于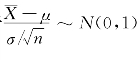，知，于是，因此，检验假设（8．1．3）的拒绝域可以设定，即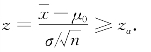

类似地，左边检验问题H 0：μ≥μ0，H 1：μ＜μ0的拒绝域为(www.xing528.com)

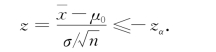
例8．1．2　微波炉在炉门关闭时的辐射量是一个重要的质量指标．某厂该质量指标服从正态分布N（μ，σ2），长期以来σ2＝0．12，且均值都符合不超过0．12的要求．为了检查近期产品的质量，抽查了25台，测得样本均值为＝0．1203，问在显著性水平α＝0．05时，炉门关闭时的辐射量是否升高了？

解　按题意需检验假设

这是右边检验问题，其拒绝域为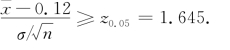

而现在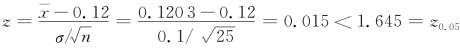，即z（根据样本算出的结果）没有落在拒绝域中，所以在显著性水平α＝0．05下，不能拒绝H 0，即可以认为当前生产的微波炉在炉门关闭时的辐射量无明显升高．

例8．1．3　某厂产品需要玻璃纸做包装，按规定供应商提供的玻璃纸的横向延伸率（是一个质量指标）不应低于65（单位）．已知该指标服从正态分布N（μ，σ2），且长期以来稳定地有σ＝5．5．从近期来货中抽查了100个样品，测得样本均值为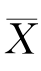＝55．06，问在显著性水平α＝0．05时能否接受这批玻璃纸？

解　若不接受这批玻璃纸，需要退货，这要慎重．因此，按题意需检验假设

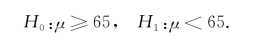
这是左边检验问题，其拒绝域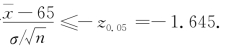

而现在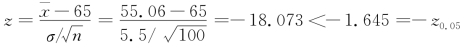，即z（根据样本算出的结果）落在拒绝域中，因此在显著性水平α＝0．05下，拒绝H 0，即不能接受这批玻璃纸．

综上所述，可得处理参数的假设检验问题的步骤如下：

（1）根据实际问题的要求，提出原假设H 0和备择假设H 1；

（2）给定显著性水平α和样本容量n；

（3）确定检验统计量和拒绝域的形式；

（4）按P｛当H 0为真时拒绝H 0｝≤α求出拒绝域；

（5）取样，根据样本观察值作出决策，是接受H 0还是拒绝H 0．