概率论与数理统计（第5版）：假设检验的基本思想

先结合一个例子，来说明假设检验的基本思想和做法．

例8．1．1　根据以往经验知道，某自动包装机在正常的情况下包装的袋装某食品的重量X服从正态分布，其均值为0．5（kg），标准差为0．015．某天开工后为检查此包装机是否正常，随机地抽取它所包装的9袋食品，测得其净重量为：0．497，0．506，0．518，0．524，0．498，0．511，0．520，0．515，0．512．问是否可以认为此包装机正常？

以μ，σ分别表示总体X的均值和标准差，由于长期实践表明标准差比较稳定，我们就设σ＝0．015．于是X～N（μ，0．0152），这里μ未知．问题是根据样本观察值来判断μ＝0．5还是μ≠0．5．为此，我们提出两个相互对立的假设

然后，我们要给出一个合理的法则，根据这个法则，利用已知样本作出决策——是接受假设H 0（即拒绝H 1），还是拒绝H 0（即接受H 1）．如果作出接受H 0，则认为μ＝0．5，即认为包装机工作正常，否则，认为包装机工作不正常．

由于要检验的假设涉及总体均值μ，所以首先想到能否借助样本均值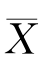这个统计量来进行判断．由于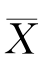是μ的无偏估计，的观察值在一定程度上反映了μ的大小．因此，如果假设H 0为真，则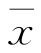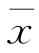与μ0的偏差|一般不应太大．如果|过分大，我们就怀疑H 0的正确性，而拒绝H 0，考虑到当H 0为真时，Z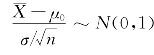＝．而衡|的小大归结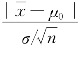|的大小（σ为已知）．

基于上面的想法，我们可以适当地选取一个正数k，使当观察值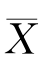满足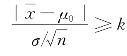时，就拒绝H 0；反之，若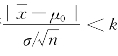时，就不能拒绝H 0．

然而，由于作出决策的依据是样本，当实际上H 0为真时，仍然可以作出拒绝H 0的决策（这种可能性是无法消除的），这是一种错误，犯这种错误的概率记为P｛当H 0为真时拒绝H 0｝．

由于无法消除犯这种错误的可能性，自然希望能够将犯这种错误的概率控制在一定的限度之内，即给出一个较小的数α（0＜α＜1），使犯这种错误的概率不超过α，即

为了确定常数k，我们考虑统计量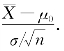由于只考虑犯错误的概率最大为α，令式（8．1．1）的右边取等号，即令P｛当H 0为真时拒绝H 0｝＝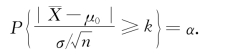

由于当H 0为真时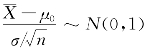，，根据标准正态分布的分位点的定义知．因此，当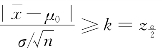时，就拒绝H 0；反之，若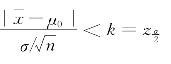时，就不能拒绝H 0．(www.xing528.com)

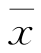例如，在例8．1．1中，取α＝0．05时，有又已知n＝9，σ＝0．015，再由样本算得＝0．511，则有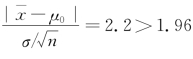，于是就拒绝H 0，认为包装机工作不正常．

通常取α＝0．01，0．05等，因此，当H 0为真时（即μ＝μ0时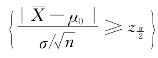），是小概率事件，根据实际推断原理就可以认为，如果H0为真，则由一次试验得到的观察值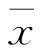满足不等式几乎是不可能的．现在在一次试验中竟然出现了满足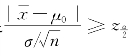的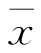，则我们有理由怀疑原来的假设H 0的正确性，因此拒绝H 0．若出现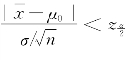，此时我们没有理由拒绝H 0，因此只能“接受”H 0．

应该注意，这里的“接受”H 0并非真正意义下的接受H 0，而是在没有理由拒绝H 0时，只能说“拒绝H 0”的证据不足，或者说冒一定的风险接受H 0．今后若无特别说明，本书中的“接受”H 0均是以上这种意义．

在例8．1．1的做法中，称α为显著性水平，统计量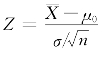称为检验统计量．

前面的假设检验问题通常可以叙述成：在显著性水平α下，检验假设

H 0称为原假设或零假设（null hypothesis），H 1称为备择假设（alternative hypothesis），即在原假设被拒绝后可供选择的假设．

当检验统计量取某个区域C中的值时，我们就拒绝H 0，则称区域C为拒绝域（它的余集称为“接受域”），拒绝域的边界称为临界点．如在例8．1．1中，拒绝域为为临界点．

上述利用Z检验统计量得到的检验法，称为Z检验法．

假设检验是运用“证明某个事物的正确性不如否定其对立面容易”的逻辑思想，通过数据和模型的矛盾来否定假设．值得注意的是，一般在假设检验中，原假设是受到保护的．