1．设总体X的分布律如下表：
其中，
是未知参数，利用总体X的如下样本值3，1，3，0，3，1，2，3，求θ的矩估计值和极大似然估计值．
2．设总体X的概率密度
式中，θ＞-1是未知参数，X 1，X 2，…，Xn是来自总体X的一个容量为n的简单随机样本，分别用矩估计法和极大似然估计法求θ的估计值和估计量．
3．（1）设X 1，X 2，…，Xn是来自总体X的一个样本，且X～P（λ）（参数为λ的泊松分布），试求未知参数λ的极大似然估计量及矩估计量，并求P｛X＝0｝的极大似然估计值；（2）某铁路局证实一个扳道员在5年内所引起的严重事故的次数服从泊松分布．求一个扳道员在5年内未引起严重事故的概率p的极大似然估计值．下表中，r表示一扳道员在5年中引起严重事故的次数，s表示观察到的扳道员人数．
4．若X 1，X 2，…，Xn是总体X的一个样本．试证明（1）
＝1）是E（X）的无偏估计量；（2）在E（X）的所有形式
的无偏估计量中，
为有效的估计．
5．设X 1，X 2，X 3，X 4是来自均值为θ的指数分布总体的样本，其中θ未知．设有估计量T 1＝
（1）指出T 1，T 2，T 3中哪几个是θ的无偏估计量；（2）在上述θ的无偏估计中指出哪一个较有效．
6．设有来自正态总体X～N（μ，0．92）容量为9的简单随机样本，测得样本均值
＝5，求未知参数μ的置信水平为0．95的置信区间．
7．若某枣树产量服从正态分布，产量方差为400kg2．现随机抽9株，产量（单位：kg）为：112，131，98，105，115，121，90，110，125，求这批枣树每株平均产量的置信水平为0．95的置信区间．(www.xing528.com)
8．随机地从一批钢珠中抽出16颗，测量它们的直径（单位：mm），并求得其样本均值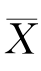
＝32．15，样本方差s2＝0．522，假设钢珠直径服从正态分布N（μ，σ2），试求置信水平为95%时μ的置信区间和置信水平为90%的σ2的置信区间．
9．为了比较A，B两种灯泡的寿命，从A型号灯泡中随机抽取80只，测得平均寿命
＝2000（h），样本标准差s1＝80（h）；从B型号灯泡中随机抽取100只，测得平均寿命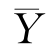
＝1900（h），样本标准差s2＝100（h）．假设两种型号的灯泡寿命均服从正态分布，A型号的灯泡寿命X～
，B型号的灯泡寿命
，且相互独立．求置信水平为0．90时两个总体方差比
的置信区间．
10．某灯泡厂某天生产了一批灯泡，从中抽取了10个进行寿命试验，得数据如下（单位：h）1050，1100，1080，1120，1200，1250，1040，1130，1300，1200．问该天生产的灯泡平均寿命大约多少？若知道该天生产灯泡寿命的方差是8，试利用切比雪夫不等式估计出灯泡平均寿命的置信区间（α＝0．05）．
11．设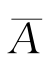
是参数θ的无偏估计，且有D（
）＞0，试证
2＝（
）2不是θ2的无偏估计．
12．试证明均匀分布
中未知参数θ的极大似然估计不是无偏的．
13．设X在［0，θ］上服从均匀分布，θ为未知参数，X 1，X 2，…，Xn是总体X的一个样本．试比较参数θ的两个无偏估计量
的有效性．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
