设已给定置信水平为1-α,并设X 1,X 2,…,Xn 1和Y 1,Y 2,…,Y n2分别是两个正态总体![]() 的样本,且这两个样本相互独立.
的样本,且这两个样本相互独立.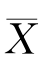 ,
, 分别为两个样本的均值,
分别为两个样本的均值,![]() 分别为两个样本的方差.
分别为两个样本的方差.
7.3.3.1 两个总体均值之差μ1-μ2的置信区间
(1)![]() 均为已知
均为已知
由于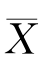 ,
,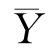 分别为μ1,μ2的无偏估计,所以
分别为μ1,μ2的无偏估计,所以 -
-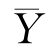 为μ1-μ2的无偏估计.由
为μ1-μ2的无偏估计.由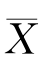 ,
,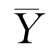 的独立性以及
的独立性以及![]() 得
得
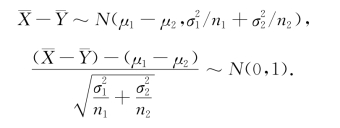
与一个总体均值的置信区间类似,得μ1-μ2的置信水平为1-α的置信区间
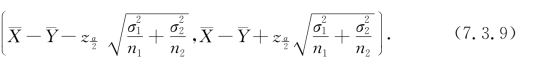
(2)![]() ,但σ2为未知
,但σ2为未知
此时,根据定理6.2.4知
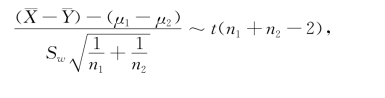
由此得μ1-μ2的置信水平为1-α的置信区间
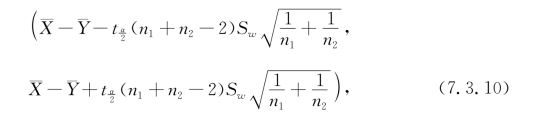
式中,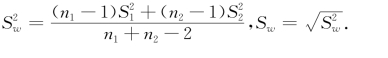
例7.3.4 2003年某地区分行业调查职工平均工资情况,已知体育、卫生、社会福利事业单位职工工资(单位:元)X~N(μ1,2182);文教、艺术、广播事业单位职工工资(单位:元)Y~N(μ2,2272).从总体X中调查25人,得到平均工资为1286元,从总体Y中调查30人,得到平均工资为1272元,求这两大行业职工平均工资之差的置信水平为0.99的置信区间.
解 按实际情况,可以认为分别来自两个总体的样本是相互独立的.又两个总体的方差已知,根据式(7.3.9)可得总体均值之差μ1-μ2的置信水平为0.99的置信区间.
已知![]()
![]() ,代入式(7.3.9),得μ1-μ2的置信水平为0.99的置信区间为
,代入式(7.3.9),得μ1-μ2的置信水平为0.99的置信区间为
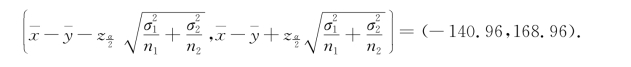
由于这个置信区间包含0,在实际中我们就可以认为这两大行业职工平均工资没有显著差异.
例7.3.5 为比较Ⅰ,Ⅱ两种型号步枪子弹的枪口速度,随机地取Ⅰ型子弹10发,得到枪口速度的平均值为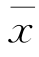 1=500m/s,标准差s 1=1.10m/s,随机地取Ⅱ型子弹20发,得到枪口速度的平均值为
1=500m/s,标准差s 1=1.10m/s,随机地取Ⅱ型子弹20发,得到枪口速度的平均值为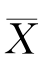 2=496m/s,标准差s 2=1.20m/s.假设两总体都服从正态分布,且由生产过程可以认为方差相等.求两总体均值差μ1-μ2的置信水平为0.95的置信区间.
2=496m/s,标准差s 2=1.20m/s.假设两总体都服从正态分布,且由生产过程可以认为方差相等.求两总体均值差μ1-μ2的置信水平为0.95的置信区间.
解 按实际情况,可以认为分别来自两个总体的样本是相互独立的.又假设两个总体的方差相等,根据式(7.3.10)可得总体均值之差μ1-μ2的置信水平为0.95的置信区间.(https://www.xing528.com)
已知1-α=0.95,α/2=0.025,n 1=10,n 2=20,n 1+n 2-2=28,t 0.025(28)=2.0484,sw=1.1688,代入式(7.3.10),得μ1-μ2的置信水平为0.95的置信区间为
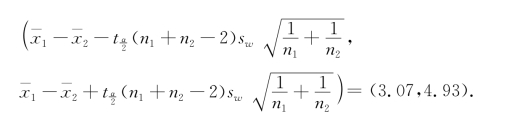
由于这个置信区间的下限大于零,在实际中我们可以认为μ1比μ2大.
7.3.3.2 两个总体方差之比![]() 的置信区间(μ1,μ2未知情形)
的置信区间(μ1,μ2未知情形)
此时根据定理6.2.4知
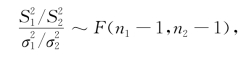
并且F(n 1-1,n 2-1)不依赖于任何参数,由此得
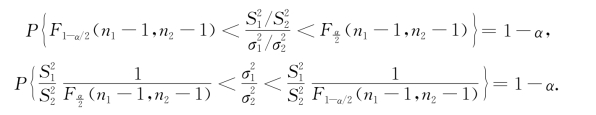
于是,得![]() 置信水平为1-α的置信区间为
置信水平为1-α的置信区间为
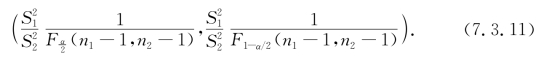
例7.3.6 研究机器A和机器B生产的钢管的内径,随机抽取机器A生产的钢管18根,测得样本方差![]() ;抽取机器B生产的钢管13根,测得样本方差
;抽取机器B生产的钢管13根,测得样本方差![]() .设两个样本独立,且由机器A和机器B生产的钢管的内径分别服从正态分布
.设两个样本独立,且由机器A和机器B生产的钢管的内径分别服从正态分布![]() 未知).试求方差之比
未知).试求方差之比![]() 的置信水平为0.9的置信区间.
的置信水平为0.9的置信区间.
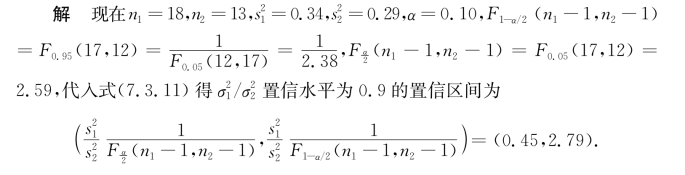
由于![]() 的置信区间包含1,在实际问题中我们可以认为σ21和σ22没有显著差别.
的置信区间包含1,在实际问题中我们可以认为σ21和σ22没有显著差别.
两个正态总体均值之差和方差之比的置信区间,见表7-2.
表7-2 两个正态总体均值之差和方差之比的置信区间(置信水平为1-α)


习题7.3.5详解
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




