单个正态总体均值和方差的置信区间

7．3．2．1　均值μ的置信区间

设已给定置信水平为1-α，并设X 1，X 2，…，X n是总体N（μ，σ2）的样本，，S 2分别为样本均值和样本方差．

（1）σ2为已知

此时，由例7．3．1已经给出了μ的置信水平为1-α的置信区间为

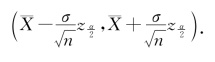
（2）σ2为未知

此时，不能由式（7．3．3）给出区间估计，因其含有未知参数σ．考虑到S 2是σ2的无偏估计，将式（7．3．2）中的σ换成，根据定理6．2．3知

并且式（7．3．5）的右边不依赖于任何未知参数，按t分布的上侧α分位点的定义，有

这样，我们就得到了μ的置信水平为1-α的置信区间

例7．3．2　设有一大批产品，现从中随机抽取16个，其质量如下：506，508，499，503，504，510，497，512，514，505，493，496，506，502，509，496（单位：g）．设该产品的质量服从正态分布，求总体均值μ的置信水平为0．95的置信区间．

解　这里，由所给数据算得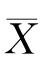＝503．75，s＝6．2022．根据式（7．3．6）得μ的置信水平为0．95的置信区间为

(www.xing528.com)

7．3．2．2　方差σ2的置信区间（μ未知的情形）

由于S 2是σ2的无偏估计，根据定理6．2．2知，

并且上式的右边不依赖于任何未知参数，按χ2分布的上侧α分位点的定义，有

即

这样，我们就得到了σ2的置信水平为1-α的置信区间

σ的置信水平为1-α的置信区间为

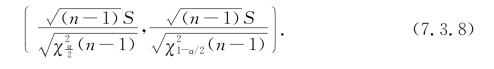
例7．3．3　求例7．3．2中标准差σ的置信水平为0．95的置信区间．

解　根据例7．3．2知，＝503，s＝6．2022，1-α＝0．95，α／2＝0．025，n-1＝15，查表得根据式（7．3．8）得σ的置信水平为0．95的置信区间为（4．58，9．60）．一个正态总体均值和方差的置信区间，见表7-1．

表7-1　一个正态总体均值和方差的置信区间（置信水平为1-α）