【摘要】:,X n是总体X的样本,且总体均值E=μ和方差D=σ2存在,证明当n>1时,μ的无偏估计量比μ的无偏估计量X 1有效.证明由于,所以当n>1时,D(X 1)=,即比X 1有效.无偏性和有效性都是在样本容量n固定的前提下给出的.我们自然希望随着样本容量的增大,一个估计量的值稳定于待估参数的真值.这样,估计量又有下述一致性的要求.定义7.2.3设(X 1,X 2,…
现在来比较参数θ的两个无偏估计量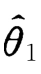 和
和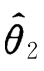 ,如果在样本容量相同的情况下,1的观察值比2更密集在真值θ的附近,我们就认为
,如果在样本容量相同的情况下,1的观察值比2更密集在真值θ的附近,我们就认为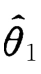 比
比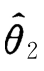 理想.由于方差是随机变量的取值与其数学期望的偏离程度的度量,所以无偏估计量以方差小者为好,这就引出了有效性这个概念.
理想.由于方差是随机变量的取值与其数学期望的偏离程度的度量,所以无偏估计量以方差小者为好,这就引出了有效性这个概念.
定义7.2.2 设![]() 和
和![]() 都是θ的无偏估计量,若对于任意的θ∈Θ,有D(
都是θ的无偏估计量,若对于任意的θ∈Θ,有D(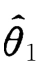 )<D(
)<D(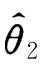 ),则称
),则称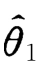 比
比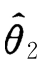 有效.
有效.
例7.2.4 设X 1,X 2,…,X n是总体X的样本,且总体均值E(X)=μ和方差D(X)=σ2存在,证明当n>1时,μ的无偏估计量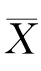 比μ的无偏估计量X 1有效.
比μ的无偏估计量X 1有效.
证明 由于![]() ,所以当n>1时,D(X 1)=
,所以当n>1时,D(X 1)=![]() ,即
,即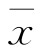 比X 1有效.
比X 1有效.
无偏性和有效性都是在样本容量n固定的前提下给出的.我们自然希望随着样本容量的增大,一个估计量的值稳定于待估参数的真值.这样,估计量又有下述一致性的要求.
定义7.2.3 设(X 1,X 2,…,Xn)为参数θ的估计量,当n→+∞时,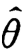 (X 1,X 2,…,Xn)依概率收敛于θ,则称为θ的一致性估计量(或相合估计量),有时也简称为一致估计量.(https://www.xing528.com)
(X 1,X 2,…,Xn)依概率收敛于θ,则称为θ的一致性估计量(或相合估计量),有时也简称为一致估计量.(https://www.xing528.com)
即,对于任意的ε>0,有
则称为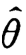 为θ的一致估计量.
为θ的一致估计量.
例7.2.5 设X 1,X 2,…,Xn是来自总体X的样本,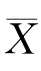 是样本均值,证明:
是样本均值,证明: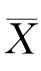 是总体均值E(X)的一致估计量.
是总体均值E(X)的一致估计量.
证明 根据定理5.1.2(切比雪夫大数定律),在![]() ,即样本均值
,即样本均值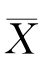 依概率收敛于总体均值E(X).
依概率收敛于总体均值E(X).
根据一致估计量的定义,样本均值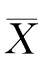 是总体均值E(X)的一致估计量.
是总体均值E(X)的一致估计量.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




