无偏性及样本矩的无偏估计量

定义7．2．1　设X 1，X 2，…，Xn是总体X的一个样本，θ∈Θ，若估计量＝的数学期望E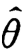（）存在，且对任意的θ∈Θ，有，则称为θ的无偏估计量．

称为以作为θ的估计的系统误差．无偏估计的实际意义就是无系统误差．

例如，设总体X的均值μ和方差σ2均未知，根据例6．1．3知，E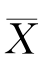（）＝μ，E（S 2）＝σ2．这就是说，不论总体服从什么分布，样本均值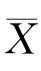是总体均值的无偏估计量；样本方差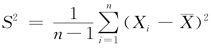是总体方差σ2的无偏估计量，而估计量不是总体方差σ2的无偏估计量．

例7．2．1　设X在［0，θ］上服从均匀分布，θ为未知参数．问θ的估计量＝2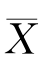是否为θ的无偏估计量．

解　由于X 1，X 2，…，X n是总体X的样本，所以它们与总体X同分布，于是

根据数学期望的性质，有

因此，估计量＝2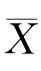是θ的无偏估计量．(https://www.xing528.com)

例7．2．2　设总体X的k阶矩μk＝E（X k）存在（k≥1），又设X 1，X 2，…，Xn是X的一个样本．证明不论总体服从什么分布，样本的k阶矩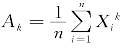是总体k阶矩μk的无偏估计量．

证明　由于X 1，X 2，…，Xn与总体X同分布，所以1，2，…，n，即，因此Ak是μk的无偏估计量．

例7．2．3　设从均值μ，方差σ2＞0的总体中，分别抽取容量为n 1和n 2的两个独立样本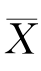， 1和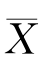 2分别为两个样本均值．试证明，对于任意的常数a，b（a＋b＝1），Y＝a 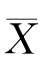1＋b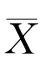 2都是μ的无偏估计量，并确定常数a，b使D（Y）达到最小．

解　（1）由于E（Y）＝aE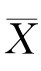（ 1）＋bE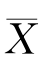（ 2）＝（a＋b）μ＝μ，所以对于任意的常数a，b（a＋b＝1），Y＝a 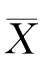1＋b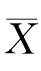 2都是μ的无偏估计量．

（2），以下在a＋b＝1时，求a和b使D（Y）达到最小．以下给出两种解法．