矩估计法及其应用于概率统计

设X为连续型随机变量，其概率密度为f（x；θ1，θ2，…，θk），或X为离散型随机变量，其分布律为P｛X＝x｝＝p（x；θ1，θ2，…，θk），其中，θ1，θ2，…，θk为待估参数，X 1，X 2，…，X n是总体X的一个样本．假设总体X的前k阶矩存在，即对X为连续型随机变量，有

对X为离散型随机变量，有

l＝1，2，…，k．其中，RX是x可能取值的范围．

基于样本矩依概率收敛于相应的总体矩μl（l＝1，2，…，k），样本矩的连续函数依概率收敛于相应的总体矩的连续函数（见6．1．3节内容），我们就用样本矩作为相应的总体矩的估计量．这种估计方法称为矩估计法．

矩估计法的具体做法如下，设

这是一个包含k个未知参数θ1，θ2，…，θk的联立方程组．一般来说可以从中解出θ1，θ2，…，θk，得到

用Ai分别代替上式中的μi（i＝1，2，…，k），即以i＝θi（A 1，…，Ak）分别作为θi（i＝1，2，…，k）的估计量，这种估计量称为矩估计量．矩估计量的观察值称为矩估计值．

例7．1．2　设X在［0，θ］上服从均匀分布，θ为未知参数．X 1，X 2，…，Xn是总体X的一个样本，求θ的矩估计量．

解　由于X在［0，θ］上服从均匀分布，所以总体X的一阶矩为μ1＝E（X）＝，又样本的一阶矩，令A 1＝μ1，则，因此θ的矩估计量为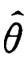＝2．

例7．1．3　设总体X服从参数为θ的指数分布，其概率密度为(www.xing528.com)

式中，θ＞0，X 1，X 2，…，Xn是总体X的一个样本，求θ的矩估计量．

解　根据例4．1．3知总体X的一阶矩为E（X）＝θ，从而得到方程θ＝因此，θ的矩估计量为

例7．1．4　设总体X的均值μ和方差σ2都存在，且σ2＞0，但μ和σ2均为未知．X 1，X 2，…，X n是总体X的一个样本，求μ和σ2的矩估计量．

解　由于总体X的一阶、二阶矩分别为μ1＝E（X）＝μ，μ2＝E（X 2）＝D（X）＋［E（X）］2＝σ2＋μ2，解得

用Ai分别代替上式中的μi（i＝1，2），得到μ和σ2的矩估计量分别为

这个结果表明，总体X的均值μ和方差σ2的矩估计量的表达式与总体具体服从什么分布无关，即无论总体X服从什么分布，只要均值和方差存在，则例7．1．4的结论都是成立的．

例如，X～N（μ，σ2），μ和σ2未知，根据例7．1．4，μ和σ2的矩估计量分别为

参数的矩估计法在估计总体的均值、方差等数字特征时，不必知道总体的分布类型，非常直观、简便，这是矩估计法的优点．但矩估计法也存在不足，在总体分布类型已知的情况下，矩估计法没有充分利用总体分布所提供的信息，因此可能导致它的精度比其他估计法低．