正态总体下的抽样定理

设总体X的均值为μ，方差为σ2，X 1，X 2，…，Xn是来自总体X的一个样本，，S 2为样本均值与样本方差，根据例6．1．3有

根据例3．4．3后面的说明，有限个相互独立的正态随机变量的线性组合仍然服从正态分布（正态分布的可加性），于是有，若X～N（μ，σ2），则也服从正态分布．综合以上所述，可以得到下面的定理：

定理6．2．1　设X 1，X 2，…，Xn是来自正态总体N（μ，σ2）的样本，是样本均值，则有

例6．2．6　设X 1，X 2，…，X 6是来自总体X～N（52，6）的样本，求样本均值落在50．8到53．8之间的概率．

解　由于X 1，X 2，…，X 6是来自总体X～N（52，6）的样本，根据定理6．2．1，则～N（52，6／6），于是Y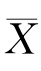＝-52～N（0，1），因此

对于正态总体N（μ，σ2）的样本均值与样本方差S 2，有如下定理：

定理6．2．2　设X 1，X 2，…，Xn是来自正态总体N（μ，σ2）的样本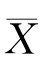，，S 2分别为样本均值与样本方差，则有

（1）

（2）与S 2独立．

定理6．2．2的证明，这里从略（其证明见：何书元《概率论与数理统计》）．

定理6．2．1和定理6．2．2合在一起，称之为Fisher引理．以下将要介绍的两个定理可以作为Fisher引理的两个推论．

定理6．2．3　设X 1，X 2，…，Xn是来自正态总体N（μ，σ2）的样本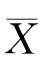，，S 2分别为样本均值与样本方差，则有

证明　根据定理6．2．1和定理6．2．2，有

且二者独立．根据t分布的定义，有

对于两个正态总体的样本均值与样本方差，有以下定理：

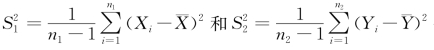定理6．2．4　设X 1，X 2，…，Xn1和Y 1，Y 2，…，Y n2分别是来自正态总体N（μ1，和的样本，且两个样本相互独立．设分别是这两个样本的均值；分别是这两个样本的方差，则有

（1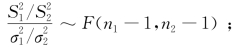）(www.xing528.com)

（2）当时，

式中,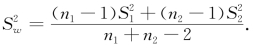

证明　（1）根据定理6．2．2，有

由于两个样本相互独立，所以和独立，由F分布的定义，有

即

（2）根据定理6．2．1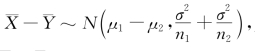，则

又，且它们相互独立，根据χ2分布的可加性，有

可以证明U和V相互独立，根据t分布的定义，有

式中，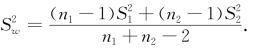

本节给出的3个重要分布和4个抽样定理，在以下几章中起着重要的作用．

例6．2．7　设X 1，X 2，…，X 10是来自总体X～N（μ，4）的样本，求样本方差S 2大于2．622的概率．

解　根据定理6．2．2，得，根据题意，所求概率为

查表得，由上侧α分位点的意义，有

例6．2．8　设两个正态总体X，Y的方差分别为，在总体X，Y中分别抽取容量为n 1＝61，n 2＝31的样本，且两个样本相互独立，样本方差分别为

解　根据定理6．2．4，得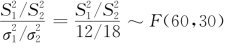，因此

查表知F 0．05（60，30）＝1．74，根据上侧α分位点的意义，有