概率论与数理统计（第5版）：3个重要分布

定义6．2．1　统计量的分布称为抽样分布．

下面介绍3个来自正态分布的常用统计量的分布．

6．2．1．1　χ2分布

定义6．2．2　设X 1，X 2，…，Xn是来自总体N（0，1）的样本，则称统计量

服从自由度为n的χ2分布，记为χ2～χ2（n）．

此处，χ2分布的自由度是指独立的随机变量的个数．

自由度为n的2分布的概率密度为

式中，是Gamma函数，概率密度f（x）的图形如图6-2所示．

可以证明χ2分布具有以下性质．

图6-2　χ2分布概率密度的图形

（1）若X 1，X 2，…，X n相互独立，都服从N（0，1），则χ2（n）．反之，若X～χ2（n），则X可以分解为n个相互独立的标准正态随机变量的平方和．

（2）若X～χ2（n），则有E（X）＝n，D（X）＝2n．

（3）χ2分布具有可加性．设X～χ2（n 1），Y～χ2（n 2），并且X和Y相互独立，则有X＋Y～χ2（n 1＋n 2）．

应该说明，对有限个相互独立的服从χ2分布的随机变量，χ2分布的可加性也是成立的．

定义6．2．3　若χ2～χ2（n），对于给定的α，0＜α＜1，称满足条件

的点为χ2（n）的上侧α分位点，其中f（x）为χ2分布的概率密度，其图形如图6-3所示．计算的MATLAB程序，见本书附录B的例B．2．5的（2）．

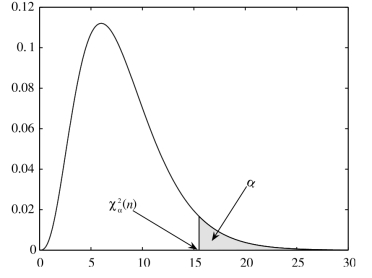
图6-3　χ2（n）的上侧α分位点

对于不同的α，n，的值已编制成表供查用，见书末的附表4——χ2分布表．例如，α＝0．1，n＝25，查χ2分布表，得＝34．382．但该表只列到n＝45为止，Fisher曾证明，当n充分大时，近似地有，其中zα是标准正态分布的上侧α分位点．因此，当n＞45时，可以利用上述近似公式计算例如，（由更详细的表得χ2 0．05（50）＝

例6．2．1　设X 1，X 2，…，X 10是来自总体X～N（0，0．32）的样本，求

解　由于X 1，X 2，…，X 10是来自总体X～N（0，0．32）的样本，则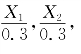都服从N（0，1）．

根据χ2分布的定义，有，因此，有

这是因为，当n＝10，＝16时，查χ2分布表，得α＝0．1．

例6．2．2　设X 1，X 2，…，X 6是来自总体X～N（0，1）的样本，Y＝（X 1＋X 2＋X 3）2＋（X 4＋X 5＋X 6）2，求常数c，使cY服从χ2分布．

解　由于X 1，X 2，…，X 6是来自总体X～N（0，1）的样本，则有X 1＋X 2＋X 3～N（0，3），所以

同理，X 4＋X 5＋X 6～N（0，3），所以X 3和X 4＋X 5＋X 6相互独立，根据χ2分布的定义，

于是，

即当时，cY服从χ2分布．

6．2．1．2　t分布

定义6．2．4　设X～N（0，1），Y～χ2（n），且X，Y相互独立，则称统计量

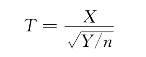
服从自由度为n的t分布，记为T～t（n）．

自由度为n的t分布的概率密度为

图6-4是几个不同的自由度n对应的概率密度f（x）的图形．

图6-4　t分布概率密度的图形

可以证明t分布具有以下性质：

（1）若X～N（0，1），Y～χ2（n），且X，Y相互独立，则．反之，若T～t（n），则有相互独立的X～N（0，1），Y～χ2（n），使

（2）t分布与标准正态分布有如下关系：(www.xing528.com)

式中，f n（x）为自由度是n的t分布的概率密度，φ（x）为标准正态分布的概率密度．这个性质说明t分布的极限分布是标准正态分布．

定义6．2．5　若t～t（n），对于给定的α，0＜α＜1，称满足条件

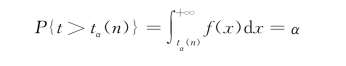
的点tα（n）为t（n）的上侧α分位点，其中f（x）为t分布的概率密度，其图形如图6-5所示．

图6-5　t（n）的上侧α分位点

t分布的上侧α分位点的值，可以查书末附录C的附表3——t分布表．例如，对于α＝0．05，n＝10，查t分布表得t 0．05（10）＝1．8125．计算tα（n）的MATLAB程序，见附录B的例B．2．5的（3）．

根据t分布的上侧α分位点的定义以及t分布的概率密度f（x）的对称性，可知t 1-α（n）＝-tα（n）．根据t分布与标准正态分布的关系，当n＞45时，可以用近似公式tα（n）≈zα，其中zα是标准正态分布的上侧α分位点．

例6．2．3　设X 1，X 2，…，X 5是来自总体X～N（0，1）的样本，求常数c，使统计量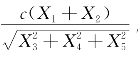服从t分布．

解　由于X 1，X 2，…，X 5是来自总体X～N（0，1）的样本，所以X 1＋X 2～N（0，2）,，且二者独立，根据t分布的定义，要使

服从t分布，则有

由于X 1＋X 2～N（0，2），所以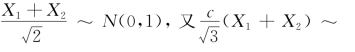N（0，1），则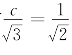，由此解得

即当

6．2．1．3　F分布

定义6．2．6　设U～χ2（n 1），V～χ2（n 2），且U，V独立，则称统计量

服从自由度为（n 1，n 2）的F分布，记为F～F（n 1，n 2）．其中，n 1称为第一自由度，n 2称为第二自由度．其概率密度为

对几个不同的自由度对应的概率密度的图形如图6-6所示．

图6-6　F分布概率密度的图形

可以证明F分布具有以下性质．

（1）若U～χ2（n 1），V～χ2（n 2），且U，V独立，则．反之，若F～F（n 1，n 2），则有相互独立的U～χ2（n 1），V～χ2（n 2），使

（2）由F分布的定义可知，若F～F（n 1，n 2），则

定义6．2．7　若F～F（n 1，n 2），对于给定的α，0＜α＜1，称满足条件

的点Fα（n 1，n 2）为F（n 1，n 2）分布的上侧α分位点，其中f（x）为F分布的概率密度，其图形如图6-7所示．

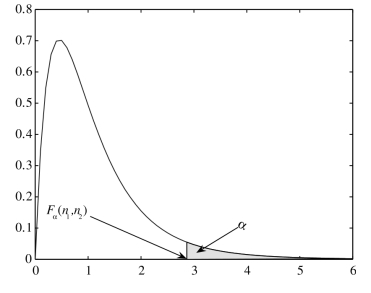
图6-7　F（n 1，n 2）的上侧α分位点

F分布的上侧α分位点的值，可以查书末的附录C附表5——F分布表．例如，对于α＝0．05，n 1＝9，n 2＝12，查F分布表得F 0．05（9，12）＝2．80．计算Fα（n 1，n 2）的MATLAB程序，见书末附录B的例B．2．5的（4）．

F分布的上侧α分位点，有如下重要的性质：

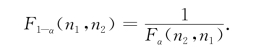
例如，

例6．2．4　已知X～t（n），证明X 2～F（1，n）．

证明　由于X～t（n），按t分布的定义和性质，X可以写成的形式，其中Z～N（0，1），Y～χ2（n），且Z与Y相互独立．

于是，在中，（n），且与Y相互独立．按F分布的定义，有

例6．2．5　设X 1，X 2，…，X 15是来自总体N（0，σ2）的样本，确定

例页码 电子书="136" 纸书="122"/>的分布．

解　由于X 1，X 2，…，X 15是来自总体N（0，σ2）的样本，所有Xi～N（0，σ2），，且它们相互独立．根据χ2分布的定义，有

而相互独立，根据F分布的定义，有