独立同分布中心极限定理

定理5．2．1（独立同分布中心极限定理）设随机变量X 1，X 2，…，Xn，…相互独立，服从同一分布，且具有数学期望和方差：E（X k）＝μ，D（X k）＝σ2＞0（k＝1，2，…），则随机变量之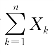的标准化随机变量

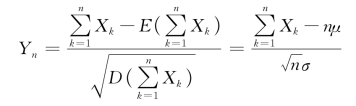
的分布函数Fn（x）对于任意的x满足

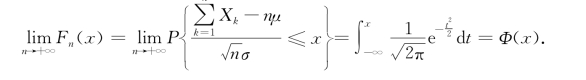
独立同分布中心极限定理说明，具有数学期望E（X k）＝μ和方差D（X k）＝σ2＞0的独立同分布的随机变量的标准化变量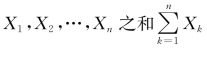，当n充分大时，有

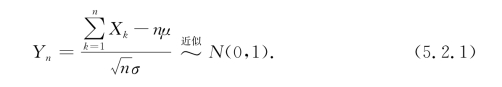
在一般情况下，很难求出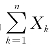的分布的确切形式．式（5．2．1）说明，当n充分大时，可以利用正态分布对进行理论分析或实际计算．

例5．2．1　设｛X i（i＝1，2，…）｝是一些相互独立同分布的随机变量，且它们都服从参数为λ的泊松分布P（λ），可以证明（证明见：何书元《概率论与数理统计》中的“泊松分布的可加性”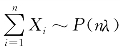）．当λ＝1时，随着n的增加（n＝1，2，5，10，15，20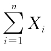）将如何变化？的标准化随机变量又将如何变化？

解　当n＝1，2，5，10，15，20和λ＝1时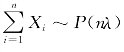，的分布律折线图如图5-2所示．

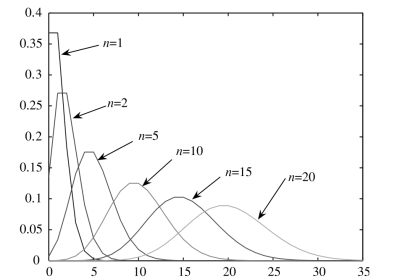
图5-2　的分布律折线图

从图5-2可以看出i的分布律折线图，随着n的增加（1→2→5→10→15→20）越来越接近正态分布密度函数的形状．即当n较大时,近似服从正态分布，因此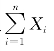的标准化随机变量近似服从标准正态分布．这就直观地验证了定理5．2．1（独立同分布中心极限定理）．(www.xing528.com)

说明：例5．2．1中分布律折线图的MATLAB程序，见本书附录B的例B．2．4．

例5．2．2　在一个超市中，结账柜台为顾客服务的时间（以min计）是相互独立的随机变量且服从相同的分布，均值为1．5，方差为1．（1）求对100位顾客的总服务时间不超过2h的概率．（2）要求总的服务时间不超过1h的概率大于0．95，问至多能为多少位顾客服务？

解　（1）设X i（i＝1，2，…，100）表示为第i位顾客的服务时间．根据题意，X 1，X 2，…，X 100相互独立且服从相同的分布，根据定理5．2．1，有

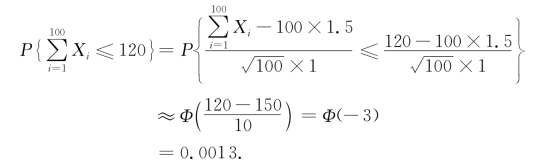
由于所求出的概率比较小，在实际中可以认为为100位顾客服务的总时间不小于2h几乎是不可能的．

（2）设1h内能为N位顾客服务，并设X i（i＝1，2，…，N）表示为第i位顾客的服务时间．根据题意，要确定最大的N，使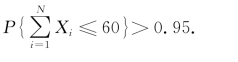

根据定理5．2．1，有

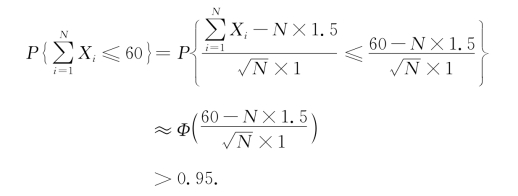
查表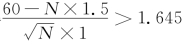，于是，得5．8，因此N＜33．64．

由于N为正整数，所以取N＝33，即最多只能为33位顾客服务，才能使总的服务时间不超过1h的概率大于0．95．