概率论与数理统计（第5版）-3个大数定律解析

定理5．1．2（切比雪夫大数定律）设随机变量X 1，X 2，…，X n，…相互独立，且具有相同的数学期望和方差：E（X k）＝μ，D（X k）＝σ2（k＝1，2，…）．作前n个随机变量的算术平，则对于任意的正数ε，有

证明　由于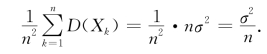根据切比雪夫不等式，有

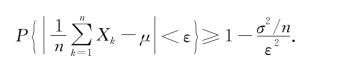
在上式中令n→＋∞，并注意到概率不能大于1，即得

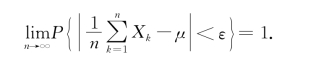
现在来解释一下式（5．1．3）的意义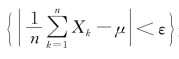是一个随机事件，式（5．1．3）表明，当n→＋∞时，这个事件的概率趋于1．即，对于任意的正数ε，当n充分大时，不等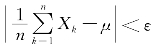成立的概率很大．

定理5．1．2表明，当n很大时，随机变量X 1，X 2，…，Xn的算术平均＝接近于数学期望E（X 1）＝E（X 2）＝…＝E（X n）＝μ．这种接近是在概率意义下的接近．通俗地说，在定理5．1．2的条件下，n个随机变量的算术平均，当n无限增加时将几乎变成一个常数．

定义5．1．1　设Y 1，Y 2，…，Y n，…是一个随机变量序列，a是一个常数．若对于任意的正数ε，有

则称序列Y 1，Y 2，…，Y n，…依概率收敛于a．记为

依概率收敛的序列还有以下性质．

设，又设函数g（x，y）在点（a，b）处连续，则

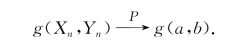
这样，定理5．1．2用“依概率收敛”又可以叙述为

定理5．1．2　设随机变量X 1，X 2，…，Xn，…相互独立，且具有相同的数学期望和方差：E（X k）＝μ，D（X k）＝σ2（k＝1，2，…），则序列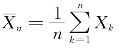依概率收敛于μ，即

例5．1．2　设随机变量X 1，X 2，…，Xn，…相互独立，且Xi（i＝1，2，…）的分布律如下表：

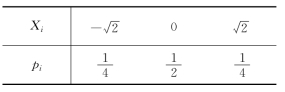
问对随机变量序列X 1，X 2，…，X n，…可否使用切比雪夫大数定律？

解　由于随机变量X 1，X 2，…，Xn，…相互独立，且E（X i）＝0，D（Xi）＝1，i＝1，2，…，因此，满足定理5．1．2的条件，可以使用切比雪夫大数定律．

定理5．1．3（伯努利大数定律）设n A是n次独立重复试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则对于任意的正数ε，有

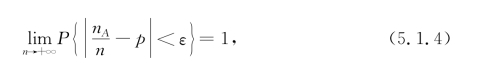
或

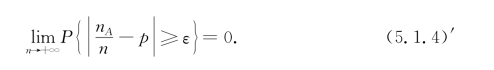
证明　由于n A～B（n，p），根据例4．2．6，有n A＝X 1＋X 2＋…＋X n，其中，X 1，X 2，…，X n相互独立，且都服从B（1，p）．因此，E（X k）＝p，D（X k）＝p（1-p），k＝1，2，…，n．根据定理5．1．2（切比雪夫大数定律），得

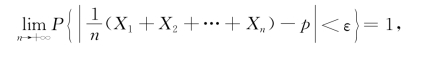(www.xing528.com)

即

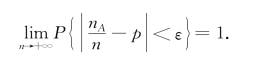
定理5．1．3（伯努利大数定律）表明，事件A发生的频依概率收敛于事件A发生的概率．它揭示了“事件发生的频率具有稳定性”．因此，在实际问题的应用中，当试验的次数很大时，用事件的频率代替它的概率是合理的．

例5．1．3　根据例1．2．1我们知道，抛一枚质地均匀的硬币出现正面的概率为0．5．以下分三种情况验证硬币出现正面的频率与概率的关系，三种情况下均进行1000组实验，每组实验次数即抛硬币的次数分别为100，1000，10000．

解　三种情况下均进行1000组实验，每组实验次数即抛硬币的次数分别为100，1000，10 000，硬币出现正面的频率与概率的偏离情况见图5-1的（1）—（4）．

从图5-1的（1）—（4）可以看出，硬币出现正面的频率与概率的偏离程度，随着抛硬币次数的增加（100→1000→10000），频率与概率的偏离程度越来越小，即频率与概率越来越接近．这就直观地验证了定理5．1．3（伯努利大数定律）．

说明：例5．1．3中三种情况下频率与概率偏离图的MATLAB程序，见本书附录B的例B．2．3．

如果事件A的概率很小，根据伯努利大数定律，事件A发生的频率也是很小的，或者说A很少发生，即“概率很小的事件在个别试验中几乎不会发生”，这一原理称为小概率事件原理（或实际推断原理），它的应用很广泛．例如，如果在某种假设下，一个事件发生的概率很小，可是它在一次试验中竟然发生了，我们根据小概率事件原理，有理由怀疑假设的正确性．但应该注意，小概率事件与不可能事件是有区别的．

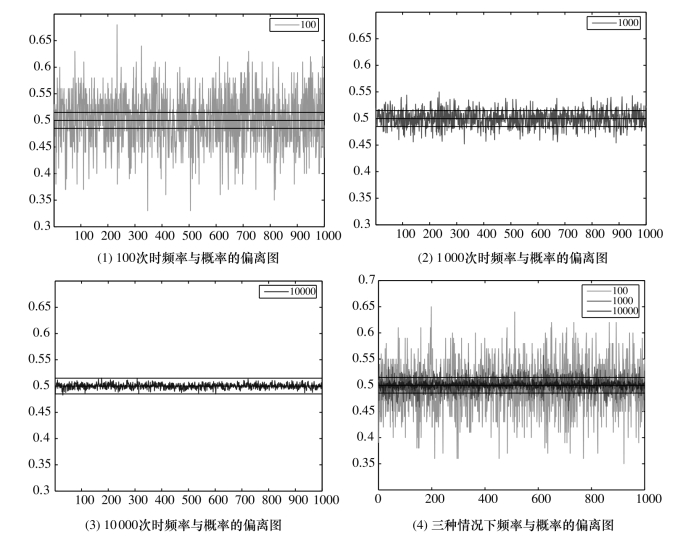
图5-1　抛硬币问题中频率与概率的关系

定理5．1．2中要求随机变量X 1，X 2，…，Xn，…的方差存在，但在这些随机变量相互独立且服从同一分布的场合，并不需要这一条件，我们有以下定理．

定理5．1．4（辛钦大数定律）设随机变量X 1，X 2，…，X n，…相互独立，服从同一分布，且具有数学期望E（X k）＝μ（k＝1，2，…），则对于任意的正数ε，有

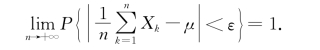
定理5．1．4的证明从略．定理5．1．2（切比雪夫大数定律）是定理5．1．4（辛钦大数定律）的特殊情形，定理5．1．4在应用中是很重要的．

*例5．1．4　设随机变量X 1，X 2，…，X n相互独立同分布，都在（0，1）区间上服从均匀分布，则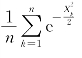依 概率收敛于

证明　由于随机变量X 1，X 2，…，Xn独立同分布，则随机变量也独立同分布．因为X k在（0，1）上服从均匀分布，其概率密度函数为f（x）＝1（0＜x＜1），则

根据定理5．1．4（辛钦大数定律），当n→＋∞时，依概率收敛于

例5．1．4　的结果在定积分的数值计算上是很有用的．

*例5．1．5　用例5．1．4的结果计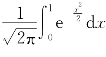（要求计算结果精确到小数点后六位数）．

解　根据例5．1．4的结果，先在计算机上产生n个（0，1）区间上的均匀分布的随机数x k（k＝1，2，…，n），然后对每一个x k计算，最后得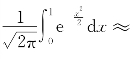其精确值和n＝1 0 0 0 0，1 0 0 0 0 0时的模拟值见下表（其MATLAB程序，见本书附录B的例B．2．10）：

当然，由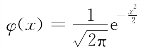是标准正态分布的概率密度函数，所以查标准正态分布表，得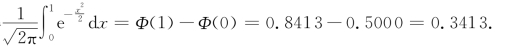

但是，一般的标准正态分布表都只有小数点后4位，有时可能精度不够．

由于可以通过线性变换将（a，b）区间上的定积分化为（0，1）区间上的定积分，所以上述计算定积分的方法具有普遍意义．这就是辛钦大数定律在蒙特卡洛（Monte Carlo）方法计算定积分方面的应用．