概率论与数理统计第5版习题4解析

复习题4．9详解

1．设随机变量X的概率密度为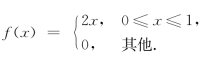求E（X），D（X）．

2．设相互独立随机变量X 1，X 2，X 3的数学期望分别为2，1，4，方差分别为9，20，12．求X 1-2X 2＋5X 3的数学期望和方差．

3．某地方电视台在体育节目中插播广告有3种方案（10s、20s和40s）供业主选择，据一段时间内的统计，这3种方案被选择的可能性分别是10%，30%和60%．（1）设X为业主随机选择的广告时间长度，求E（X），并说明E（X）的含义．（2）假设该电视台在体育节目中插播10s广告售价是4000元，20s广告售价是6500元，40s广告售价是8000元．若设Y为广告价格，请写出Y的概率分布，计算E（Y），并说明E（Y）的含义．

4．设某种商品的需求量X（t）是服从区间［10，30］上的均匀分布的随机变量，而经销商店进货数量为区间［10，30］中的某一个数，商店每销售1t产品可获利500元，若供大于求，则削价处理，每处理1t商品亏损100元；若供不应求，则可从外部调剂供应，此时1t商品仅获利300元，为使商店获利期望值不少于9280元，试确定最小进货量．

5．若抛n颗均匀骰子，求n颗骰子出现点数之和的数学期望与方差．

6．设连续型随机变量X的概率密度为

已知，求常数a，b，c的值．

7．设电压（以V计）X～N（0，9），将电压施加于一检波器，其输出电压为Y＝5X 2，求输出电压Y的均值．

8．设随机变量X服从参数为λ的泊松分布，且已知E［（X-1）（X-2）］＝1，求λ．

9．设X为随机变量，C为常数，证明D（X）＜E（X-C）2，对于C≠E（X）（说明：由于D（X）＝E［X-E（X）］2，上式表明E（X-C）2当C＝E（X）时取到最小）．

10．将一枚硬币重复掷n次，以X和Y分别表示正面向上和反面向上的次数，求X和Y的相关系数．(www.xing528.com)

11．设随机变量（X，Y）的分布律为

验证X与Y不相关，但X与Y不是相互独立的．

12．游客乘电梯从底层到电视塔顶层观光，电梯于每个整点的第5min，25min和55min从底层起行．假设一游客在早8点的第X min到达底层候梯处，且X在［0，60］上均匀分布，求该游客等候时间的数学期望．

复习题4．13详解

13．设随机变量（X，Y）的概率密度为

求：（1）E（X），E（Y），E（XY）；（2）D（X），D（Y）；（3）Cov（X，Y）；（4）ρXY；（5）（X，Y）的协方差矩阵．

14．设随机变量X的分布律，试证明X的数学期望不存在．

15．对于随机变量X，Y，Z，已知E（X）＝E（Y）＝1，E（Z）＝-1，D（X）＝D（Y）＝D（Z）＝，求E（X＋Y＋Z），D（X＋Y＋Z）．

16．假设随机变量U在区间［-2，2］上服从均匀分布，随机变量

求：（1）X和Y的联合分布律；（2）D（X＋Y）．