独立性与不相关性在概率论与数理统计（第5版）中

定义4．3．2　当ρXY＝0时，称X和Y不相关．

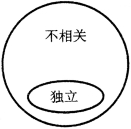
图4-1　不相关与独立的关系示意图

假设随机变量X和Y的相关系数ρXY存在，当X和Y相互独立时，根据数学期望的性质（4）及协方差的计算公式（4．3．1），知Cov（X，Y）＝0，从而ρXY＝0，即X和Y不相关．反之，若X和Y不相关，X和Y却不一定相互独立（见下面的例4．3．3）．由此可见，“独立”必然导致“不相关”，而“不相关”不一定导致“独立”．不相关与独立的关系示意图，如图4-1所示．

不过，从以下的例4．3．4可以看到，当（X，Y）是二维正态分布时，X和Y不相关与X和Y相互独立是等价的．

例4．3．3　设（X，Y）的分布律见表4-3．

表4-3　（X，Y）的分布律

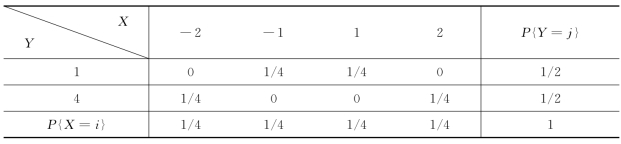
根据表4-3易知E（X）＝0，E（Y）＝5／2，E（XY）＝0，于是ρXY＝0，即X和Y不相关，这表明X和Y不存在线性关系．但P｛X＝-2，Y＝1｝＝0≠P｛X＝-2｝P｛Y＝1｝，知X和Y不是相互独立的．事实上，X和Y具有关系Y＝X 2．

例4．3．4　设（X，Y）服从二维正态分布，它的概率密度为

(www.xing528.com)

求X和Y的相关系数．

解　根据例3．2．4，知道（X，Y）关于X和Y的边缘概率密度分别为

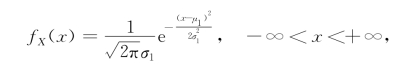
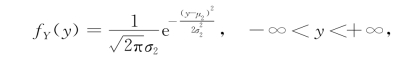
所以，

根据本节习题6，

这说明，二维正态分布（X，Y）的概率密度中的参数ρ就是X与Y的相关系数，因而二维正态随机变量的分布完全可由X与Y各自的数学期望、方差以及它们的相关系数决定．

在第3章已经讲过，若（X，Y）服从二维正态分布，那么X与Y相互独立的充分必要条件为ρ＝0．由于ρ＝ρXY，所以对二维正态分布（X，Y）来说，X与Y不相关和X与Y相互独立是等价的．