概率统计中的协方差与相关系数

我们在方差的性质（3）的证明中已经看到，如果两个随机变量X与Y是相互独立的，则有E｛［X-E（X）］［Y-E（Y）］｝＝0．

这意味着当E｛［X-E（X）］［Y-E（Y）］｝≠0时，随机变量X与Y不是相互独立的，而存在着一定的关系．

定义4．3．1　如果随机变量X与Y的数学期望和方差都存在，称

为随机变量X与Y的协方差（covariance），记为Cov（X，Y）＝E｛［X-E（X）］［YE（Y）］｝．当D（X）＞0，D（Y）＞0时，

称为随机变量X与Y的相关系数（correlation coefficient）．

按定义4．3．1，若（X，Y）是离散型随机变量，其分布律为P｛X＝x i，Y＝y j｝＝pij（i，j＝1，2，…），则

若（X，Y）是连续型随机变量，其概率密度为f（x，y），则

根据定义4．3．1，可知Cov（X，Y）＝Cov（Y，X），Cov（X，X）＝D（X）．

根据定义4．3．1和方差的性质，对于任意的随机变量X与Y，有D（X±Y）＝D（X）＋D（Y）±2Cov（X，Y）．

定理4．3．1（协方差的计算公式）

证明　按协方差的定义和数学期望的性质，有

我们称式（4．3．1）为协方差的计算公式．

定理4．3．2（协方差的性质）（1）Cov（aX，bY）＝ab Cov（X，Y），其中，a，b是常数；（2）Cov（X 1＋X 2，Y）＝Cov（X 1，Y）＋Cov（X 2，Y）．

证明　（1）根据协方差的计算公式，有

（2）根据协方差的计算公式，有

例4．3．1　设（X，Y）的分布律如下表：

求Cov（X，Y），ρXY．

解　根据X和Y的联合分布律，则X和Y的边缘分布律分别如下表：

则(https://www.xing528.com)

根据协方差的计算公式，有

根据相关系数的定义，有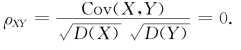

例4．3．2　设（X，Y）的概率密度为

求Cov（X，Y），ρXY．

解　根据（X，Y）的概率密度和数学期望的定义，有

同理，又

则

根据协方差的计算公式，有

根据相关系数的定义，有

以下给出相关系数ρXY的两个性质，并说明ρXY的含义．

考虑以X的线性函数a＋bX来近似表示Y．我们以均方误差

来衡量a＋bX近似表示Y的好坏程度．e的值越小表示a＋bX与Y的近似程度越好．这样，我们就取a，b使e最小．为此，将e分别关于a，b求偏导数，并令它们为零，得

由此解得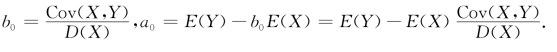

把a 0，b 0代入式（4．3．2），得

根据式（4．3．3），可以得到下述定理（证明从略）．

定理4．3．3　（1）|ρXY|≤1；（2）|ρXY|＝1的充分必要条件是，存在a，b使P｛Y＝a＋bX｝＝1．

由式（4．3．3）知，均方误差e是|ρXY|的严格单调减少函数，这样ρXY的含义就很明显了．当|ρXY|较大时，e较小，表明X与Y（就线性关系来说）联系较为紧密．特别地，当|ρXY|＝1时，由定理4．3．3的（2）知，X与Y之间以概率1存在线性关系．于是ρXY是一个用来表征X与Y之间线性关系紧密程度的量．当|ρXY|较大时，我们通常说X与Y线性相关的程度较好；当|ρXY|较小时，我们说X与Y线性相关的程度较差．