常见分布方差分析-概率论与数理统计第5版

例4．2．2　设随机变量X服从0-1分布，其分布律为P｛X＝0｝＝1-p，P｛X＝1｝＝p，求D（X）．

解　由于E（X）＝0·（1-p）＋1·p＝p，E（X 2）＝02·（1-p）＋12·p＝p，根据方差的计算公式，有

例4．2．3　设X～P（λ），求D（X）．

解　X的分布律为

由于在例4．1．5中已经得到E（X）＝λ，而

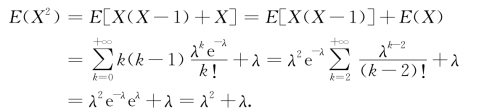
根据方差的计算公式，有D（X）＝E（X 2）-［E（X）］2＝（λ2＋λ）-λ2＝λ．

例4．2．4　设X～U（a，b），求D（X）．

解　X的概率密度为

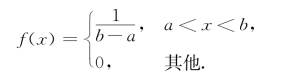
由于在例4．1．6中已经得到，根据方差的计算公式，有

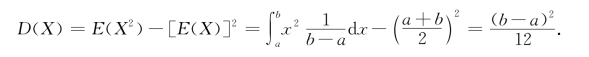
例4．2．5　设X服从参数为θ的指数分布，其概率密度为

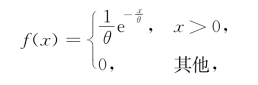
式中，θ＞0．求D（X）．

解　根据例4．1．3，有E（X）＝θ，根据定理4．1．1，有

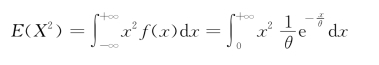
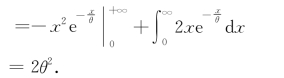
根据方差的计算公式，有D（X）＝E（X 2）-［E（X）］2＝2θ2-θ2＝θ2．

例4．2．6　设X～B（n，p），求E（X）和D（X）．

解　根据二项分布的定义，随机变量X是n重伯努利试验中事件A发生的次数，且在每次试验中事件A发生的概率为p．引进随机变量

易知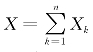，且X k只依赖第k次试验，而各次试验相互独立，于是X 1，X 2，…，X n相互独立，又X k（k＝0，1，2，…，n）服从0-1分布（或2点分布），其分布律如下表：

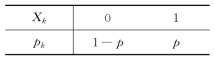
根据例4．2．2，E（X k）＝p和D（X k）＝p（1-p），k＝0，1，2，…，n．根据数学期望的性质，有(www.xing528.com)

根据方差的性质，有

例4．2．7　设X～N（μ，σ2），求E（X）和D（X）．

解　根据例4．2．1，是X的标准化随机变量，则E（Z）＝0，D（Z）＝1．由，得X＝σZ＋μ，于是E（X）＝σE（Z）＋μ＝μ，D（X）＝σ2D（Z）＝σ2．

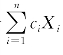根据第3章例3．4．3后面的说明（“正态分布的可加性”）知道，若Xi～N（μi，，且它们相互独立，则它们的线性组合仍然服从正态分布，且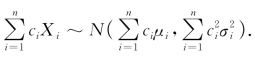．这是一个很有用的结论．

例如，设X～N（1，3），Y～N（2，4），且X与Y相互独立，则Z＝2X-3Y也服从正态分布．而E（Z）＝2×1-3×2＝-4，D（Z）＝22×3＋（-3）2×4＝48，于是Z～N（-4，48）．

通常把考试评定的（卷面）分数称为原始分数．在评定一个学生的学习成绩时，常用的做法是根据多门课程的总原始分数来评定考生的成绩．其实，这种做法不一定完全合理．由于各门课程的难易程度各不相同，评分标准宽严程度也有差别，这就反映在各门课程的分数价值是不相同的．例如，同样是80分，在得分普遍较低的课程与得分普遍较高的课程中其价值是不等的．另外，各门课程的评分体系也未必相同．例如，在某省高考中，语文、数学、英语满分是150，而理综或文综满分是300．

对于不同课程考试所得到的原始分数一般具有不同的均值和标准差，即具有不同的参照点和不同的单位．如果直接对它们进行算数运算是欠科学的，将各门课程原始分数相加作为考生总成绩也是有欠缺的．一种改进的方法是将原始分数转换成标准分数（standard score），即转换为有相同参照点和统一单位来处理．另外，根据标准分数的线性变换产生的T分数（T-score），其作用与标准分数基本相同，但它能消除标准分数中的负值，而其排序的结果与标准分数相同．

若X～N（μ，σ2），则称X的标准化为标准分数．注意，在实际计算标准分数时，用X的观察值——具体的原始分数x来计算标准分标准分数可以回答这样一个问题：“一个给定分数距离平均分有数多少个标准差？”

根据例4．2．1，则E（Z）＝0，D（Z）＝1．因此，将原始分数转换成标准分数，就得到了以零作为同一参照点，以相同的标准差作为统一单位．所以用标准分数来衡量学生成绩的相对地位比较科学合理．

例4．2．8　在某年级的统一考试中，设考试成绩服从正态分布，数学的平均成绩为μ1＝78（满分为100），标准差σ1＝7；英语的平均成绩为μ2＝62（满分为100），标准差σ2＝6．某个学生在本次统一考试中，数学得84，英语得68，请问该学生的数学和英语成绩在全年级统一考试中哪门课程成绩相对较好？

解　因为数学和英语考试成绩的标准差不同，因此直接用原始分数进行比较并不合理．需要将原始分数转换成标准分数，然后进行比较．

把该学生在全年级统一考试中数学和英语的原始分数转换成标准分数，则有

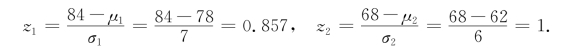
由于z 1＜z 2，所以该学生在全年级统一考试中英语成绩比数学成绩相对要好．

需要说明，以上结论与我们从原始分数出发直接比较得到的结论正好相反．

例4．2．9　在某省高考中，设考试成绩服从正态分布，有两个考生参加该省高考，语文，数学，英语，物理，化学的成绩分别为：109，121，83，113，102；124，117，100，97，95．根据该省的统计，以上五门课程平均分数分别为105，112，91，108，99，标准差分别为13，8，11，9，7．请比较以上两个考生的成绩．

解　根据原始分数可以得到标准分数和T分数（T＝10z＋103），其计算结果见表4-1．

表4-1　原始分数，标准分数和T分数

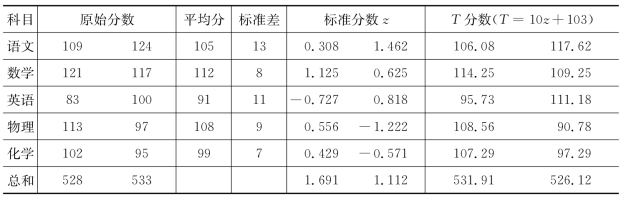
由表4-1可见，两个考生的总原始分数分别为528分和533分（前者比后者少5），而总标准分数分别为1．691和1．112（前者比后者多0．579），总T分数分别531．91分和526．12分（前者比后者多5．79）．这说明：按照总原始分数，前者比后者的成绩差；而按照总标准分数（或总T分数），前者比后者的成绩好．

因此，按照总原始分数与总标准分数（或总T分数）排序，可能使排序的结果不同．上表中最后一列T分数，取T＝10z＋103，主要是为了消除标准分数中的负值，并尽可能使T分数与原始分数接近．引入T分数可以有不同的方法，但其排序的结果都与标准分数相同．

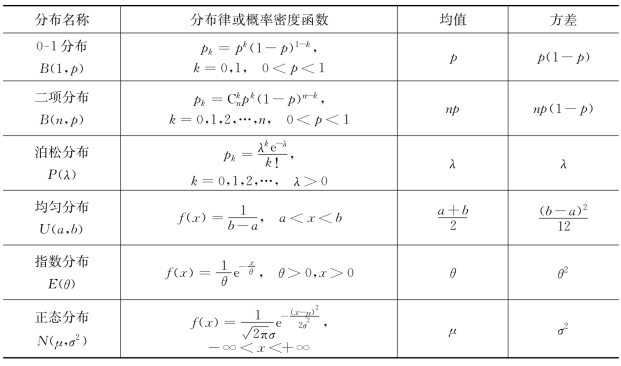
常见分布的均值和方差见表4-2．

表4-2　常见分布的均值和方差