随机变量函数数学期望的计算

在很多问题中，所研究的随机变量常常依赖于另一个随机变量．例如，一个零件的横截面是一个圆，圆的直径X是一个随机变量，那么，这个横截面的面积Y也是随机变量，且如果已知X的概率密度，要求Y（X的连续函数）的数学期望E（Y），一种方法是先求出Y的概率密度，然后按定义4．1．1求出Y的数学期望E（Y），但这样做比较麻烦．为了用简便的方法求随机变量Y的数学期望，给出以下定理．

定理4．1．1　设随机变量Y是随机变量X的连续函数Y＝g（X），则有：

（1）设X是离散型随机变量，其分布律为P｛X＝x k｝＝p k，k＝1，2，…．若级数绝对收敛，则

（2）设X是连续型随机变量，其概率密度为f（x），若积绝对收敛，则

这个定理的重要意义在于，当我们要求E（Y）时，不必算出Y的分布律或概率密度，而只需（按定理4．1．1）利用X的分布律或概率密度就可以了．

定理4．1．1可以推广到两个或两个以上随机变量函数的情形．

定理4．1．2　设随机变量Z是随机变量X，Y的连续函数Z＝g（X，Y），则有：

（1）设二维随机变量（X，Y）为离散型随机变量，其分布律为P｛X＝x i，Y＝y j｝＝p ij，i，j＝1，2，…．若级绝对收敛，则

（2）设二维随机变量（X，Y）为连续型随机变量，其概率密度为f（x，y），若积分绝对收敛，则

例4．1．7　已知随机变量X的分布律如下表：

求E（X 2＋1）和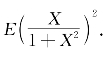

解　根据定理4．1．1，得

例4．1．8　设随机变量（X，Y）的概率密度为(www.xing528.com)

求

解　根据定理4．1．2，得

例4．1．9　某公司计划开发一种新产品市场，并试图确定该产品的产量．估计出售1kg产品可获利m元，而积压1kg产品导致n元的损失．再者，预测销售量Y（kg）服从指数分布，其概率密度为

式中，θ＞0．问若要获得利润的数学期望最大，应生产多少产品（m，n，θ均为已知）？

解　设生产x kg产品，则利润Q为x的函数

Q是随机变量，它是Y的函数，其数学期望为

令

得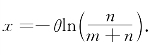而

故当时，E（Q）取得极大值，且可知这也是最大值．

例如，若

即θ＝10000，且有m＝500元，n＝2000元，则

所以，当生产2231．44kg产品时，获得利润的数学期望最大．