概率论与数理统计：数学期望的定义

定义4．1．1　（1）设离散型随机变量X的分布律为P｛X＝x k｝＝p k，k＝1，2，…，若级数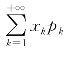绝对收敛，则称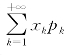为随机变量X的数学期望（expectation），记为E（X），即

（2）设连续型随机变量X的概率密度为f（x），若积分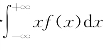绝对收敛，则称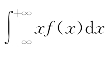为随机变量X的数学期望，记为E（X），即E（X）＝．数学期望简称期望，又称均值．

例4．1．2　甲、乙两人进行打靶，所得分数分别记为X 1，X 2，它们的分布律分别如下表：

试评定他们成绩的好坏．

解　按离散型随机变量数学期望的定义，得

因此，E（X 1）＞E（X 2），即甲的成绩比乙好．

例4．1．3　设某电子产品的寿命X服从指数分布，其概率密度为

式中，θ＞0，求E（X）．

解　根据连续型随机变量数学期望的定义，得

这个结果说明，该产品的平均寿命E（X）＝θ．

例4．1．4　某商店对某种家用电器的销售采用先使用后付款的方式．记使用寿命为X（以年计），且规定：X≤1，每台付款1500元；1＜X≤2，每台付款2000元；2＜X≤3，每台付款2500元；X＞3，每台付款3000元．设这种家用电器的寿命X服从指数分布，其概率密度为(www.xing528.com)

求该商店每台电器收费Y的数学期望．

解　先求出X落在各个时间区间的概率

根据以上计算，每台电器收费Y的分布律如下表：

因此，E（Y）＝2732．15，即平均每台电器收费2732．15元．

例4．1．5　设X～P（λ），求E（X）．

解　X的分布律为按离散型随机变量数学期望的定义，得

例4．1．6　设X～U（a，b），求E（X）．

解　X的概率密度为

按连续型随机变量数学期望的定义，得