例3.4.4 设二维随机变量(X,Y)的分布律如下表.求Z=max{X,Y}的分布律.

解 由于Z=max{X,Y}的可能取值为0,1,则有

所以,Z=max{X,Y}的分布律为

例3.4.5 设X和Y是两个相互独立的随机变量,它们的分布函数分别是F X(x)和FY(y),求M=max{X,Y}及N=min{X,Y}的分布函数.
解 (1)由于P{M≤z}=P{X≤z,Y≤z},又,X与Y是相互独立的,于是有

(2)与(1)类似,可得N=min{X,Y}的分布函数为

以上结果容易推广到n个相互独立的随机变量的情形.设X 1,X 2,…,Xn是n个相互独立的随机变量,它们的分布函数分别为F Xi(x),i=1,2,…,n,则M=max{X 1,X 1,…,Xn}及N=min{X 1,X 1,…,Xn}的分布函数分别为

特别地,当X 1,X 2,…,Xn相互独立且具有相同的分布函数F(x)时,有F max(z)=[F(z)]n,F min(z)=1-[1-F(z)]n.
例3.4.6 设系统L由2个相互独立的子系统L 1和L 2联接而成,联接的方式分别为(1)串联,(2)并联,(3)备用(当系统L 1损坏时,系统L 2开始工作),如图3-5所示.设L 1和L 2的寿命分别为X和Y,已知它们的概率密度分别为
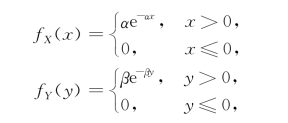

图3-5 子系统的联接方式(https://www.xing528.com)
式中,α>0,β>0且α≠β.试分别就以上3种联接方式求出系统L的寿命Z的概率密度.
解 (1)串联情况.由于当L 1和L 2中有一个损坏时,系统L就停止工作,所以,此时系统L的寿命为Z=min{X,Y}.根据L 1和L 2的寿命的概率密度,可以得到L 1和L 2的寿命的分布函数分别为

则Z=min{X,Y}的分布函数为

所以,Z=min{X,Y}的概率密度为
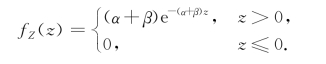
(2)并联情况.由于当且仅当L 1和L 2都损坏时,系统L才停止工作,所以,此时系统L的寿命为Z=max{X,Y}.则Z=max{X,Y}的分布函数为
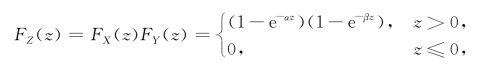
所以,Z=max{X,Y}的概率密度为

(3)备用情况.由于此时当系统L 1损坏时,系统L 2开始工作,因此,此时系统L的寿命为Z=X+Y.
当z≤0时,f Z(z)=0.
当z>0时,根据卷积公式,得

因此,Z=X+Y的概率密度为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




