Z=X+Y的分布：概率论与数理统计第5版成果

3．4．1．1　离散型随机变量和的分布

例3．4．1　已知随机变量X和Y的联合分布律如下表：

求Z＝X＋Y的分布律．

解　根据X和Y的联合分布律，Z＝X＋Y的可能取值是0，1，2，3，则Z＝X＋Y的分布律为

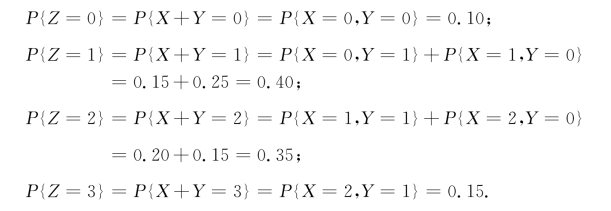
把上述计算结果列成下表：

3．4．1．2　连续型随机变量和的分布

例3．4．2　设二维连续型随机变量（X，Y）的概率密度为f（x，y），求Z＝X＋Y的概率密度．

解　（1）先求Z＝X＋Y的分布函数．

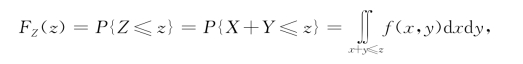
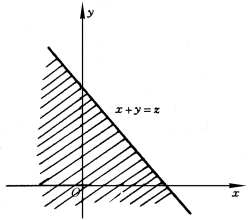
图3-4　积分区域

这里，积分区域G＝｛（x，y）|x＋y≤z｝是直线x＋y＝z及其左下方的半平面，如图3-4所示．

化累次积分，得

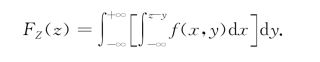
固定z和y，作变量替换，令x＝u-y，得

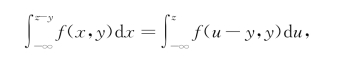
于是

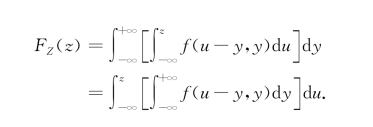(https://www.xing528.com)

（2）再求Z＝X＋Y的概率密度．

根据分布函数和概率密度的关系，得Z＝X＋Y的概率密度

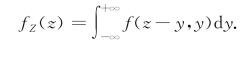
由X和Y的对称性，f Z（z）又可以写成

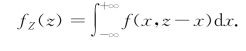
特别地，当X与Y相互独立时，设（X，Y）关于X和Y的边缘概率密度为f X（x），f Y（y），则有

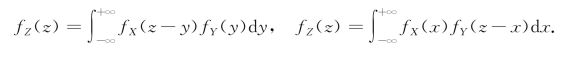
这两个公式称为卷积公式，记为f X*f Y，即

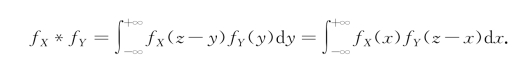
例3．4．3　设X和Y是相互独立的随机变量，它们都服从N（0，1），其概率密度为

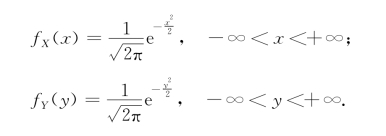
求Z＝X＋Y的概率密度．

解　根据卷积公式，得Z＝X＋Y的概率密度

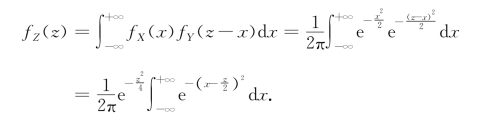
令，得

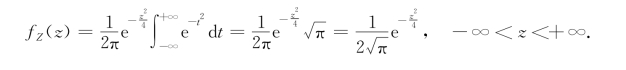
即Z＝X＋Y服从N（0，2）．

一般地，设X和Y相互独立,，则Z＝X＋Y仍然服从正态分布，且这个结论可以推广到n个相互独立的正态随机变量之和的情形．即且它们相互独立，则Z＝X 1＋X 2＋…＋Xn仍然服从正态分布，且

更一般地，可以证明，有限个相互独立的正态随机变量的线性组合仍然服从正态分布，即，且它们相互独立，则Z＝c 1X 1＋c 2X 2＋…＋cn X n仍然服从正态分布（c 1，c 2，…，cn不全为零），且Z～N（c 1μ1＋c 2μ2＋…＋．称这个性质为正态分布的可加性．