【摘要】:对于二维离散型随机变量(X,Y),有与一维离散型随机变量X的分布函数比较,得X的分布律同样,Y的分布律为,记定义3.2.2分别称p i·(i=1,2,…
对于二维离散型随机变量(X,Y),有
与一维离散型随机变量X的分布函数![]() 比较,得X的分布律
比较,得X的分布律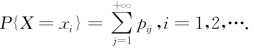 同样,Y的分布律为
同样,Y的分布律为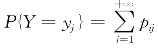 ,记
,记
定义3.2.2 分别称p i·(i=1,2,…)和p·j(j=1,2,…)为二维离散型随机变量(X,Y)关于X和关于Y的边缘分布律.
例3.2.1 设袋中装有3个球,分别标有号码1,2,3,从中随机取1个球,不放回袋中,再随机取1个球,用X,Y分别表示第1次和第2次取得的球的号码,求X和Y的联合分布律以及边缘分布律.
解 (X,Y)的可能取值为数组:(1,2),(1,3),(2,1),(2,3),(3,1),(3,2),根据乘法公式,得
具体计算结果见下表.(https://www.xing528.com)
根据上表得X和Y的边缘分布律,分别见以下2个表所列.
例3.2.2 设一个整数N等可能地在1,2,…,10这10个值中取1个值.设D=D(N)是能整除N的正整数的个数,F=F(N)是能整除N的素数的个数(注意1不是素数).试写出D和F的联合分布律,并求边缘分布律.
解 先将试验的样本点及D,F的取值情况列出,见下表:
D的所有可能取值为1,2,3,4;F的所有可能取值为0,1,2.容易得到(D,F)取(i,j)的概率(i=1,2,3,4,j=0,1,2),例如,![]()
![]() ,可得D和F的联合分布律以及边缘分布律,如下表所列.
,可得D和F的联合分布律以及边缘分布律,如下表所列.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




