二维连续随机变量及其性质

定义3．1．4　对于以F（x，y）为分布函数的二维随机变量（X，Y），如果存在非负函数f（x，y）使对于任意的x，y，有

则称（X，Y）为二维连续型随机变量，其中，函数f（x，y）称为（X，Y）的概率密度函数，或称为X和Y的联合概率密度函数．

按定义3．1．4，f（x，y）有以下性质．

（1）非负性．f（x，y）≥0．

（2）正则性．

（3）设G是xOy平面上的区域，则随机点（X，Y）落在G内的概率为

（4）若f（x，y）在点（x，y）连续，则有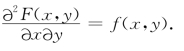

在几何上，z＝f（x，y）表示空间的一张曲面．根据性质（2），介于f（x，y）和xOy平面的空间区域的体积为1．根据性质（3），P｛（X，Y）∈G｝的值等于以G为底、以曲面z＝f（x，y）为顶面的曲顶柱体的体积．

例3．1．3　设二维随机变量（X，Y）具有概率密度

求：（1）常数A；（2）概率P｛0≤X＜1，0≤Y＜2｝．(www.xing528.com)

解　（1）根据联合密度函数的性质（2），有

由此得A＝6．

（2）根据联合密度函数的性质（3），有

例3．1．4　设二维随机变量（X，Y）具有概率密度

求F（x，y）．

解　当x≤1或y≤1时，f（x，y）＝0，则F（x，y）＝0．

当x＞1，y＞1时，

所以有

以上关于二维随机变量的讨论，不难推广到n（n＞2）维随机变量的情形．一般地，设E是一个随机试验，它的样本空间为Ω，X 1，X 2，…，X n是定义在Ω的n个一维随机变量，由它们构成的一个n维向量（X 1，X 2，…，X n）叫做n维随机向量，或n维随机变量．与二维随机变量的情形类似，也可以定义n维随机变量的分布函数等．