定义3.1.1 设E是一个随机试验,它的样本空间Ω,ω∈Ω,X=X(ω)和Y=Y(ω)是定义在样本空间Ω上的随机变量,由它们构成的一个向量(X,Y),叫做二维随机向量或二维随机变量.
第2章讨论的随机变量也叫一维随机变量.我们用定义在同一个样本空间Ω上的2个一维随机变量X和Y分别表示炮弹弹着点的横坐标和纵坐标,则弹着点的位置可用二维随机变量(X,Y)来表示.
定义3.1.2 设(X,Y)是二维随机变量,对于任意的实数x,y,二元函数
![]()
称为二维随机变量(X,Y)的分布函数,或称为随机变量X和Y的联合分布函数.
如果将二维随机变量(X,Y)看成是平面上随机点的坐标,那么,分布函数F(x,y)在(x,y)处的函数值就是随机点(X,Y)落在以点(x,y)为顶点而位于该点左下方的无穷矩形域内的概率,如图3-1所示.
根据上述解释,借助于图3-2,容易算出随机点(X,Y)落在矩形[x 1<x≤x 2,y 1<y≤y 2]内的概率为
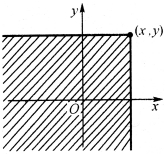
图3-1 无穷矩形
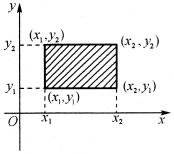
图3-2 矩形(https://www.xing528.com)

分布函数F(x,y)的性质如下:
(1)F(x,y)是变量x或y的不减函数,即对于任意固定的y,当x 2>x 1时,F(x 2,y)≥F(x 1,y);对于任意固定的x,当y 2>y 1时,F(x,y 2)≥F(x,y 1).
(2)0≤F(x,y)≤1,且对于任意固定的y,F(-∞,y)=0;对于任意固定的x,F(x,-∞)=0;F(-∞,-∞)=0,F(+∞,+∞)=1.
事实上,按定义3.1.2,对于任意固定的x,有F(x,-∞)=P{X≤x,Y<-∞}=P(∅)=0,F(+∞,+∞)=P{X<+∞,Y<+∞}=P(Ω)=1.
(3)F(x,y)=F(x+0,y),F(x,y)=F(x,y+0),即F(x,y)关于x右连续,关于y也右连续.
(4)对于任意的(x 1,y 1),(x 2,y 2),x 1<x 2,y 1<y 2,下述不等式成立:
![]()
这个性质可以由式(3.1.1)及概率的非负性得到.
类似于一维随机变量,对于二维随机变量,我们也只讨论二维离散型随机变量和二维连续型随机变量.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




