概率论与数理统计（第5版）-常见连续型随机变量

下面介绍3种重要的连续型随机变量．

2．3．2．1　均匀分布

定义2．3．2　如果连续型随机变量X的概率密度为

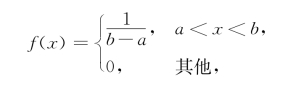
则称X在区间（a，b）上服从均匀分布（uniform distribution），记为X～U（a，b）．

根据均匀分布的概率密度，易知

在区间（a，b）上服从均匀分布的随机变量X，具有下述意义的等可能性，即它落在区间（a，b）中任意等长度的子区间内的概率只依赖于子区间的长度，而与子区间的位置无关．

事实上，对于任意长度为l的子区间（c，c＋l），a≤c，c＋l≤b，有

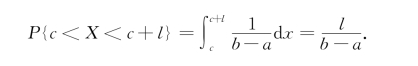
根据均匀分布的定义，容易得到它的分布函数为

f（x）和F（x）的图形分别如图2-6和图2-7所示．

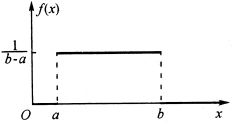
图2-6　f（x）的图形

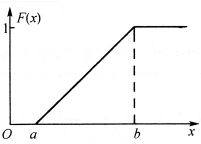
图2-7　F（x）的图形

例2．3．2　设长途客车到达某一个中途停靠站的时间T在12点10分至12点45分之间是等可能的，某旅客于12∶20到达该车站，等候20min后离开，求他在这段时间能赶上客车的概率．

解　根据题意，客车停靠站的时间T～U［10，45］，其概率密度为

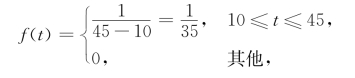
所求概率为

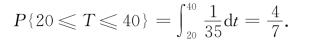
2．3．2．2　指数分布

定义2．3．3　如果连续型随机变量X的概率密度为

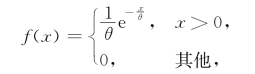
式中，θ＞0为常数，则称X服从参数为θ的指数分布（exponential distribution），记为X～E（θ）．

令λ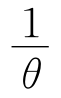＝，则上述指数分布的概率密度为

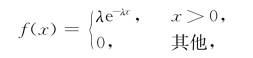
其中，λ＞0为常数，则称X服从参数为λ的指数分布，记为X～E（1／λ）．这是指数分布概率密度的另一种形式．

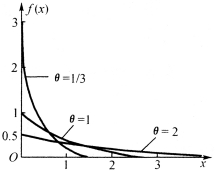
图2-8　f（x）的图形

根据指数分布的概率密度，易知f（x）≥0且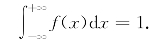

图2-8画出了和θ＝2时f（x）的图形．

根据指数分布的概率密度，易得到它的分布函数为

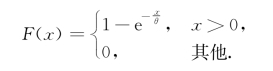
服从指数分布的随机变量X具有以下有趣的性质．

性质2．3．1　对于任意的s，t＞0，有P｛X＞s＋t|X＞s｝＝P｛X＞t｝．

证明　设X～E（θ），则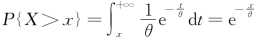，根据条件概率的定义，得

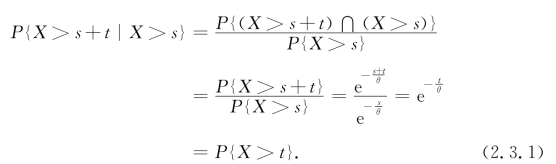
这个性质称为“无记忆性”．如果X是某元件的寿命，那么，性质2．3．1表明，已知元件已使用了s h，它总共至少使用（s＋t）h的条件概率，与开始使用时算起它至少使用t h的概率相等．就是说，元件对它使用过s h没有记忆．具有这一性质是指数分布有广泛应用的重要原因．

指数分布在可靠性理论和排队论中有重要应用，如电子元件的寿命、随机服务系统的服务时间等，都可以用指数分布来描述．

例2．3．3　某种电子元件的寿命X（以h记）服从指数分布，其概率密度为

求此元件的寿命至少为200h的概率．

解　根据题意，所求的概率为

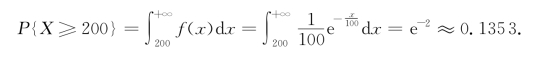
2．3．2．3　正态分布

定义2．3．4　如果连续型随机变量X的概率密度为

(www.xing528.com)

式中，μ，σ（σ＞0）为常数，则称X服从参数为μ和σ的正态分布（normal distribution），记为X～N（μ，σ2）．

根据正态分布的概率密度，易知f（x）≥0，并可以证明

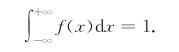
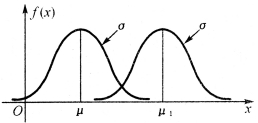
图2-9　f（x）的图形关于x＝μ对称

正态分布X～N（μ，σ2）的概率密度f（x）的图形关于x＝μ对称（图2-9），即对于任意的h＞0，有f（μ-h）＝f（μ＋h）．

当x＝μ时，f（x）取得最大值f（μ）

根据正态分布X～N（μ，σ2）的概率密度，可得它的分布函数

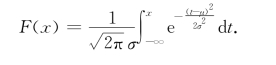
特别地，当μ＝0，σ＝1时，得到X～N（0，1），此时，称X服从标准正态分布．其概率密度函数和分布函数分别用φ（x）和Φ（x）表示（它们的图形见附录B的图B-1），即

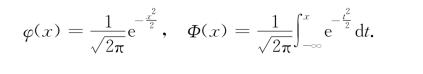
并且有Φ（-x）＝1-Φ（x）．事实上，由于φ（x）是偶函数，所以

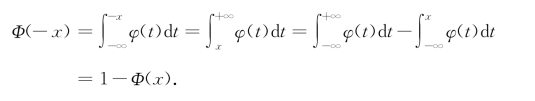
定理2．3．1　若X～N（μ，σ2），则．

证明的分布函数为

令，得

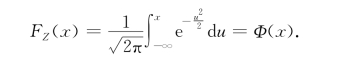
由此可知

推论2．3．1　若X～N（μ，σ2），则有：（1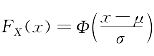；（2）对于任意区间（x 1，x 2］，有

证明　（1）若X～N（μ，σ2），根据定理2．3．1，则有

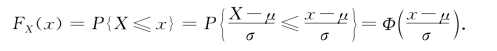
（2）若X～N（μ，σ2），根据（1），对于任意区间（x 1，x 2］，有

例2．3．4　（1）若X～N（1，4），求P｛0＜X≤1．6｝；（2）若X～N（μ，σ2），求P｛μ-kσ＜X≤μ＋kσ｝（k＝1，2，3）．

解　（1）根据推论1，查书末的附表1——正态分布表，得

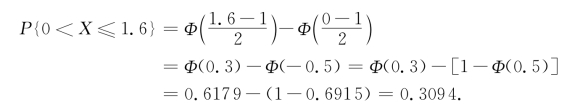
（2）若X～N（μ，σ2），根据推论1，查表得（图2-10）：

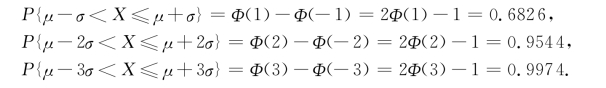
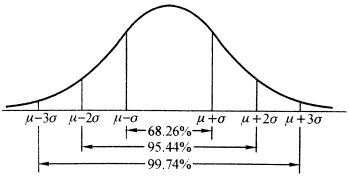
图2-10　例2．3．4的插图

我们看到，尽管正态随机变量的取值范围是（-∞，＋∞），但它的值落在（μ-3σ，μ＋3σ）内几乎是肯定的，这就是人们所说的“3σ”法则．顺便提一下，前几年比较流行“6σ管理”，其中的6σ的本意是源于产品的不合格的概率为

但“6σ管理”演绎出的是一种管理的理念．

例2．3．5　在某类人群中，假定人们的体重X～N（55，102）（单位：kg），任意选一人，试求：（1）他的体重在区间［45，65］内的概率；（2）他的体重大于85的概率．

解　（1）根据推论1并查表，得

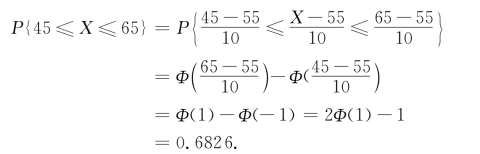
（2）根据推论1并查表，得

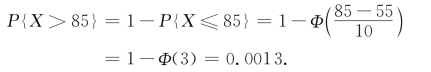
定义2．3．5　设X～N（0，1），若zα满足条件P｛X＞zα｝＝α，0＜α＜1，则称点zα为标准正态分布的上侧α分位点（表2-1，图2-11）．

表2-1列出了几个常用的zα值．zα的值可查附表1——正态分布表．计算zα的MATLAB程序，见附录B的例B．2．5的（1）．

表2-1　几个常用的zα值

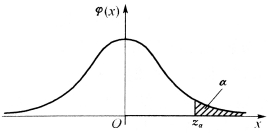
图2-11　标准正态分布的上侧α分位点

另外，由φ（x）图形的对称性知道z 1-α＝-zα．