定义2.3.1 如果对于随机变量X的分布函数F(x),存在非负可积函数f(x),使对于任意实数x,有
![]()
则称X为连续型随机变量,其中函数f(x)称为X的概率密度函数,简称概率密度(或密度函数).
在今后我们遇到的随机变量基本上是离散型或连续型随机变量,本书只讨论这两类随机变量.当然还存在非离散非连续的随机变量,见《概率论与数理统计教程》(韩明,2014).
根据定义2.3.1可知,概率密度f(x)有如下性质:
(1)非负性.f(x)≥0.
(2)正则性.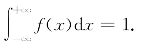
(3)对于任意的x 1,x 2(x 1<x 2),
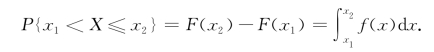
(4)若f(x)在点x处连续,则有F′(x)=f(x).
以下是关于上述4条性质的说明和几何解释.
(1)f(x)≥0,这是定义2.3.1中对f(x)的要求.
(2)根据分布函数的性质,有F(+∞)=1,另外,根据定义2.3.1,有

由性质(2)知道,介于曲线y=f(x)与Ox轴之间的面积等于1(图2-4).
(3)对于任意的x 1,x 2(x 1<x 2),有
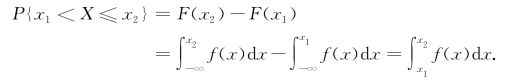
由性质(3)知道,X落在区间(x 1,x 2]上的概率P{x 1<X≤x 2}等于区间(x 1,x 2]上曲线y=f(x)之下的曲边梯形的面积(图2-5).
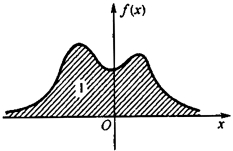
图2-4 f(x)性质(2)的插图(https://www.xing528.com)
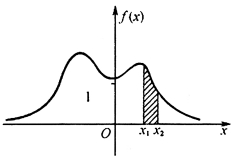
图2-5 f(x)性质(3)的插图
(4)根据“高等数学”的知识知道,在f(x)的连续点上 可导,且有F′(x)=f(x).
可导,且有F′(x)=f(x).
我们可以看到,概率密度的定义与物理学中的线密度的定义相类似,这就是f(x)为什么被称为概率密度的缘故.
例2.3.1 设随机变量X具有概率密度

(1)确定常数k;(2)求X的分布函数F(x);(3)求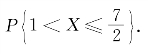
解 (1)由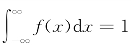 ,得
,得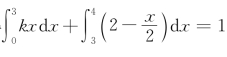 ,解得
,解得![]() ,于是,X的概率密度为
,于是,X的概率密度为
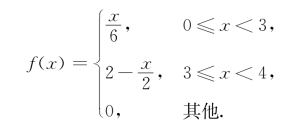
(2)X的分布函数为
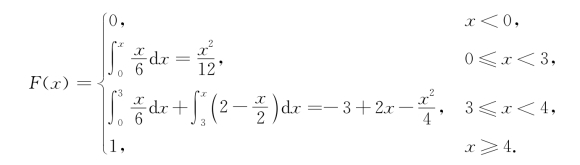
(3)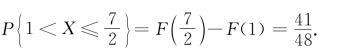
需要指出的是,对于连续型随机变量X来说,它取任意一个指定的实数a的概率均为0,即P{X=a}=0.事实上,设X的分布函数为F(x),Δx>0,则由{X=a}⊂{a-Δx<X≤a},得
![]()
在上述不等式中,令Δx→0,并注意到X是连续型随机变量,其分布函数F(x)是连续的,即得P{X=a}=0.
因此,对于连续型随机变量X来说,有
![]()
这给有关连续型随机变量计算概率带来很多方便.而对于离散型随机变量,这个性质是不存在的,离散型随机变量计算概率要“点点计较”.
注意,事件{X=a}并非不可能事件,但P{X=a}=0.我们知道,若A为不可能事件,则有P(A)=0;反之,若P(A)=0,并不一定意味着A为不可能事件.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




