以下介绍3种重要的离散型随机变量.
2.1.3.1 0-1分布
定义2.1.3 设随机变量X只可能取0与1两个值,X取1的概率为p,则X的分布律为
![]()
则称X服从0-1分布(或两点分布).
0-1分布的分布律也可以写成如下表的形式:

对于一个随机试验,如果它的样本空间只包含2个元素,即Ω={ω1,ω2},我们总能在Ω上定义一个服从0-1分布的随机变量
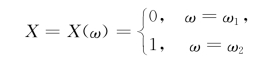
来描述这个随机试验的结果.例如,检查产品的质量是否合格,抛硬币出现的结果是正面还是反面等,都可以用0-1分布来描述.
2.1.3.2 二项分布
在1.4.2中我们介绍过伯努利试验、n重伯努利试验以及二项概率.用X表示n重伯努利试验中事件A发生的次数,则X是一个随机变量,它的所有可能取值为0,1,2,…,n.根据1.4.2的结果,n重伯努利试验中事件A发生k次的概率为![]() ,记q=1-p,则有
,记q=1-p,则有
![]()
式中,0<p<1.
定义2.1.4 如果随机变量X的分布律由式(2.1.2)给出,则称X服从参数为n,p的二项分布(binomial distribution),记为X~B(n,p).
根据二项分布的定义,显然有
(1)P{X=k}≥0,k=0,1,2,…,n;
(2)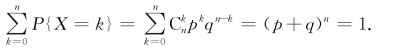
从上式可以看出,![]() 恰好是二项式(p+q)n的展开式中含有p k的那一项,因此,我们称随机变量X服从二项分布.
恰好是二项式(p+q)n的展开式中含有p k的那一项,因此,我们称随机变量X服从二项分布.
特别地,当n=1时,式(2.1.2)变为![]() ,此时,二项分布退化为0-1分布(或两点分布),记为X~B(1,p).
,此时,二项分布退化为0-1分布(或两点分布),记为X~B(1,p).
例2.1.4 某人进行射击,设每次射击命中的概率为0.02,独立射击400次,试求至少击中2次的概率.
解 将一次射击看作是一次伯努利试验,设400次射击中命中的次数为X,则有X~B(400,0.02),根据式(2.1.2)得![]() 0,1,2,…,400.
0,1,2,…,400.
于是,所求的概率为
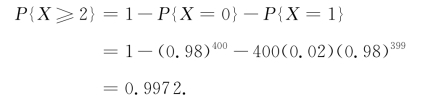
从例2.1.4中我们看到,尽管这个人射击命中的概率很小,但射击400次至少击中2次的概率很接近1.这个例子在我们日常生活中有什么启发呢?请读者思考.
例2.1.5 设有80台同类型设备,各台工作是相互独立的,发生故障的概率都是0.01,且1台设备的故障由1个人处理.考虑2种配备维修工人的方法,其一是由4人分别维护,每人负责20台;其二是由3人共同维护80台.试比较这2种方案在设备发生故障时不能及时维修的概率的大小.
解 按第1种方案.用X表示“1个人维护20台中同一时刻发生故障的台数”,则X~B(20,0.01).用Ai(i=1,2,3,4)表示事件“第i人维护的20台中发生故障时不能及时维修”,则80台中发生故障时不能及时维修的概率为
![]()
由于X~B(20,0.01),则有
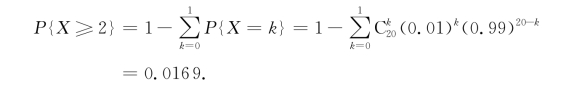
所以,有P(A 1∪A 2∪A 3∪A 4)≥0.0169.
按第2种方案.用Y表示“80台中同一时刻发生故障的台数”,则Y~B(80,0.01),于是,80台中发生故障时不能及时维修的概率为
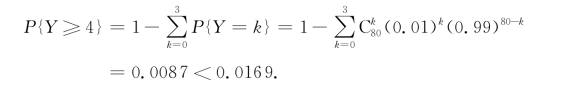
这个例子的结果说明了什么?在日常生活中对我们有什么启发?请读者思考.
2.1.3.3 泊松分布
定义2.1.5 设随机变量X的所有可能取值为0,1,2,…,而取各个值的概率为
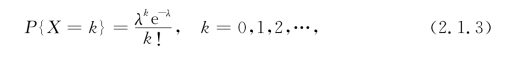
式中,λ>0为常数,则称X服从参数为λ的泊松分布(Poisson distribution),记为X~P(λ).
从泊松分布的定义,可知(https://www.xing528.com)
(1)P{X=k}≥0,k=0,1,2,…;
(2)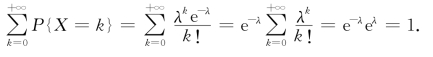
泊松分布在实际问题中具有十分广泛的应用,例如,一本书的某一页中印刷符号错误的个数;某地区一天内邮递遗失的信件数;在一段时间内,某操作系统发生故障的次数等,这些都可以用泊松分布来描述.
例2.1.6 统计资料表明,某路口每月发生交通事故次数服从参数为6的泊松分布,求该路口1个月至少发生1起交通事故的概率.
解 设该路口每月发生交通事故次数为X,根据题意X~P(6),由式(2.1.3),所求的概率为
![]()
以下给出二项分布与泊松分布的关系.
定理2.1.1(泊松定理)设λ>0是一个常数,n是任意自然数,np n=λ,则对于任意固定的非负整数k,有
![]()
定理2.1.1的证明从略.根据定理2.1.1,当n很大而p很小时,则
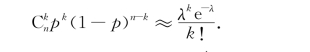
在实际计算中,当n很大,p很小时,就可以用![]() 作为
作为![]() 的近似值,而前者可以查泊松分布表(见书末附表2),计算较为方便.
的近似值,而前者可以查泊松分布表(见书末附表2),计算较为方便.
例2.1.7 比较二项分布B(200,0.025)和泊松分布P(5),并说明它们的关系.
解 以下从二项分布B(200,0.025)和泊松分布P(5)的分布律计算结果、分布律的折线图两个方面来进行比较.
(1)当n=200,p=0.025,λ=np=5时,二项分布B(n,p)和泊松分布P(λ)的分布律计算结果,见下表:

说明:在上表中![]()
![]() ,….当k≥16时,B(k;n,p)≈0,P(k;λ)≈0.
,….当k≥16时,B(k;n,p)≈0,P(k;λ)≈0.
从上表可以看出,二项分布B(200,0.025)和泊松分布P(5)的分布律计算结果接近程度比较好.
(2)二项分布B(200,0.025)和泊松分布P(5)的分布律折线图如图2-1所示.
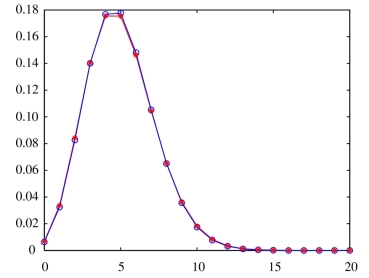
图2-1 二项分布和泊松分布的分布律折线图
说明:在图2-1中,“◦”表示二项分布B(200,0.025)的分布律,“*”表示泊松分布P(5)的分布律.
从图2-1可以看出,二项分布B(200,0.025)和泊松分布P(5)的分布律折线图接近程度比较好.
从以上(1)和(2)两个方面都说明,二项分布B(200,0.025)和泊松分布P(5)非常接近.这就直观地验证了定理2.1.1(泊松定理).
说明:例2.1.7中有关分布律的计算和折线图的MATLAB程序,见本书附录B的例B.2.2.
例2.1.8 在某一个繁忙的汽车站,有大量汽车通过,设每辆车在一天的某段时间内发生事故的概率为0.0001,在某天的该段时间内有1000辆汽车通过,求某天该段时间内发生事故的次数不小于2的概率是多少.
解 根据题意,该问题可以看作n重伯努利试验,设X为n重伯努利试验中发生事故的次数,则X~B(n,p),这里,p=0.0001,n=1000.按二项分布计算,发生事故的次数不小于2的概率为
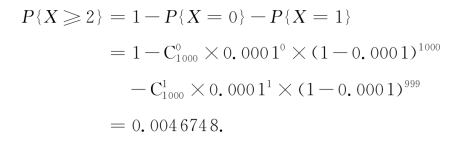
由于p=0.0001,n=1000,λ=np=0.1,所以,可以用泊松定理来近似计算.根据泊松定理,发生事故的次数不小于2的概率为
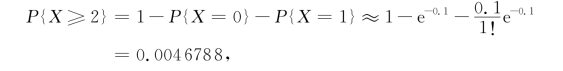
或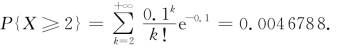
注 查书末附表2——泊松分布表,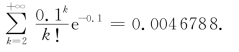
值得注意的是,按二项分布计算的结果是精确的,按泊松定理计算的结果是近似的,而这种近似计算的误差是0.000004(百万分之4).
例2.1.9 某地有2500人参加某种人寿保险,每人在年初向保险公司交付保险金200元,如果在1年内投保人死亡,则其家属可从保险公司领取5万元,设该类投保人死亡率为0.002,求保险公司获利不少于10万元的概率.
解 设X为投保人中1年内的死亡数,根据题意,X~B(n,p),这里,p=0.002,n=2500,λ=np=5,可以用泊松定理来近似计算.
如果投保人在1年内有X人死亡,则保险公司将付出50000X元,而这一年保险公司收入(元)为200×2500-50000X=500000-50000X.所求概率为
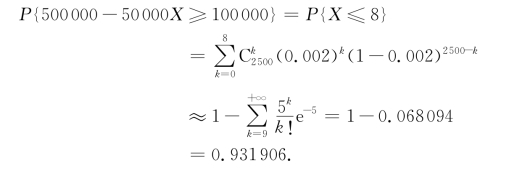
注 查书末附表2——泊松分布表,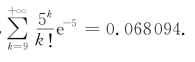
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




