【摘要】：定义2．1．2如果随机变量X的所有可能取值是有限个或可列无限多个，则称X为离散型随机变量．例如，在例2．1．1中，随机变量X的所有可能取值为0，1，2，因此它是离散型随机变量．设离散型随机变量X的所有可能取值为x k（k＝1，2，…；由于｛X＝x 1｝∪｛X＝x 2｝∪…是必然事件，且｛X＝x k｝∩｛X＝x j｝＝，k≠j（k，j＝1，2，…
定义2．1．2 如果随机变量X的所有可能取值是有限个或可列无限多个，则称X为离散型随机变量．
例如，在例2．1．1中，随机变量X的所有可能取值为0，1，2，因此它是离散型随机变量．
设离散型随机变量X的所有可能取值为x k（k＝1，2，…），X的各个可能取值的概率，即事件｛X＝x k｝的概率为
根据概率的定义，p k满足如下两个条件：
（1）p k≥0，k＝1，2，…；
（2）
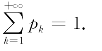
由于｛X＝x 1｝∪｛X＝x 2｝∪…是必然事件，且｛X＝x k｝∩｛X＝x j｝＝∅，k≠j（k，j＝1，2，…），于是
我们称式（2．1．1）为离散型随机变量X的分布律（或分布列）．分布律也可以用表的形式来表示，见下表：(www.xing528.com)
例2．1．2 （续例2．1．1）将一枚硬币抛掷2次，设X表示正面向上的次数，求X的分布律．
解 根据例2．1．1，有
，于是得X的分布律如下表：
例2．1．3 设一汽车在开往目的地的道路上需要经过4组信号灯，每组信号灯以
的概率允许或禁止汽车通过．以X表示汽车首次停下时，它通过的信号灯的组数（设各组信号灯的工作是相互独立的），求X的分布律．
解 用p表示每组信号灯禁止汽车通过的概率，可知X的分布律见下表：
或写成
当
时，其结果见下表：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
