在一般情况下,P(B|A)≠P(B)(这里,P(A)>0),就是说,通常情况下,事件A的发生,对事件B发生的概率是有影响的.只有在这种影响不存在时,才会有P(B|A)=P(B),此时有P(AB)=P(B|A)P(A)=P(A)P(B).
例1.4.1 试验E为“抛甲、乙两枚硬币,观察正面(H)反面(T)出现的情况”,设事件A为“甲出现H”,事件B为“乙出现H”.试验E的样本空间为Ω={HH,HT,TH,TT}.根据古典概型中概率的计算公式,得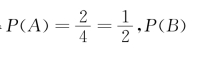

从以上的计算,我们可以看到P(B|A)=P(B),而P(AB)=P(A)P(B).事实上,根据题意,甲币是否出现正面与乙币是否出现正面是互不影响的.
定义1.4.1 设A和B是两个事件,如果满足等式
P(AB)=P(A)P(B),
则称事件A与B相互独立,简称A与B独立.
容易知道,若P(A)>0,P(B)>0,则A与B相互独立与互不相容不能同时成立(作为一个练习题,见本节的习题9).
定理1.4.1 设A和B是两个事件,且P(A)>0,若A与B相互独立,则有P(B|A)=P(B),反之亦然.
这个定理的正确性是显然的.
定理1.4.2 若事件A与B相互独立,则下列各对事件也相互独立:A与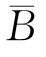 ,
,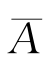 与B,
与B,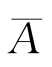 与
与 .
.
证明 由于A=AΩ=A(B∪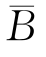 )=AB∪A
)=AB∪A ,AB∩A
,AB∩A =∅,得
=∅,得
P(A)=P(AB∪A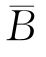 )=P(AB)+P(A
)=P(AB)+P(A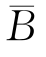 )=P(A)P(B)+P(A
)=P(A)P(B)+P(A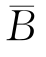 ).
).
所以,P(A )=P(A)[1-P(B)]=P(A)P(
)=P(A)[1-P(B)]=P(A)P(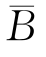 ),于是,根据定义1.4.1,A与
),于是,根据定义1.4.1,A与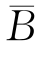 独立.由此立即推出
独立.由此立即推出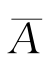 与
与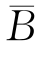 独立.再
独立.再 =B,又推出
=B,又推出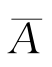 与B独立.(https://www.xing528.com)
与B独立.(https://www.xing528.com)
以下我们把2个事件的独立性推广到3个事件的情形.
定义1.4.2 设A,B,C是3个事件,如果满足等式
则称事件A,B,C相互独立.
一般地,设A 1,A 2,…,An是n(n≥2)个事件,如果对于其中任意2个,3个,…,任意n个事件的积事件的概率都等于各事件概率之积,则称事件A 1,A 2,…,An相互独立.
由此可以得到以下2个结论:
(1)若n个事件A 1,A 2,…,An(n≥2)相互独立,则其中任意k(2≤k≤n)个事件也相互独立.
(2)若n个事件A 1,A 2,…,An(n≥2)相互独立,则将A 1,A 2,…,An中任意多个事件换成它们的对立事件,所得的n个事件仍然是相互独立的.一般地,在实际应用中,对于事件的独立性常常是根据事件的实际意义去判断.
例1.4.2 某彩票每周开奖1次,每次提供10万分之一的中奖机会,如果你每周买1次彩票,尽管你坚持10年(每年52周)之久,你从未中奖的概率是多少?
解 根据题意,每次中奖的概率是10-5(10万分之一),于是,每次未中奖的概率是1-10-5.另外,10年你共买彩票520次,根据题意,每次开奖是相互独立的,因此,10年中你从未中过奖(每次都未中奖)的概率是p=(1-10-5)520≈0.9948.
从结果看,10年中你从未中过奖是很正常的事.
例1.4.3 某大学生给4家单位各发了1份求职信,假定这些单位彼此独立,通知他去面试的概率分别是![]() .问这个学生至少有1次面试机会的概率是多少.
.问这个学生至少有1次面试机会的概率是多少.
解 设Ai表示“第i个单位通知他面试”(i=1,2,3,4),则![]()
![]() ,根据题意,所求概率为
,根据题意,所求概率为
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




