全概率和贝叶斯公式解析

定义1．3．2设Ω为试验E的样本空间，B 1，B 2，…，Bn为E的一组事件．若

（1）BiB j＝∅，i≠j，i，j＝1，2，…，n；

（2）B 1∪B 2∪…∪Bn＝Ω，

则称B 1，B 2，…，Bn为样本空间Ω的一个划分（或完备事件组）．

若B 1，B 2，…，Bn为样本空间Ω的一个划分，那么，对每一次试验，事件B 1，B 2，…，Bn必有一个且仅有一个发生．

例如，设试验E为“抛掷一颗骰子观察其点数”，它的样本空间为Ω＝｛1，2，3，4，5，6｝．E的一组事件B 1＝｛1，2，3｝，B 2＝｛4，5｝，B 3＝｛6｝是Ω的一个划分，而事件组C 1＝｛1，2，3｝，C 2＝｛4，5｝，C 3＝｛5，6｝不是Ω的一个划分．

在例1．3．3中，求第2次取到白球的概率，我们将其分解为第1次取到白球或第1次取到红球2种情形，然后再用概率的有限可加性、乘法公式求得．如果袋子中有3种颜色或更多颜色的球，则式（1．3．2）可以推广为3项或多项之和的形式．在例1．3．3中利用式（1．3．2）确定P（A 2）的方法具有普遍意义，这就是以下要介绍的全概率公式．

定理1．3．2（全概率公式）设试验E的样本空间为Ω，A为E的事件，B 1，B 2，…，Bn为样本空间Ω的一个划分，且P（Bi）＞0（i＝1，2，…，n），则

式（1．3．3）称为全概率公式．

证明　由于B 1，B 2，…，Bn为样本空间Ω的一个划分，则A＝AΩ＝A（B 1∪B 2∪…∪Bn）＝AB 1∪AB 2∪…∪AB n．由于BiB j＝∅（i≠j，i，j＝1，2，…，n），则（AB i）（AB j）＝∅（i≠j；i，j＝1，2，…，n）．

根据概率的有限可加性和乘法公式，得

全概率公式的基本思想是将复杂的事件划分为若干简单情形，其直观含义是，如果每个Bi（i＝1，2，…，n）发生的概率P（Bi）以及A发生的条件概率P（A|Bi）（i＝1，2，…，n）都易于求出，则由全概率公式可以求得A的概率．

例1．3．4　设在n张彩票中有1张奖券，求第2个人摸到奖券的概率．

解　设Ai＝“第i个人摸到奖券”（i＝1，2），现在要求P（A 2）．因为A 1是否发生直接关系到A 2发生的概率，即

又，A1和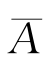 1可以构成样本空间的一个划分，根据全概率公式，得

本例的结果说明了什么？请读者思考．(www.xing528.com)

定理1．3．3（贝叶斯公式）设试验E的样本空间为Ω，A为E的事件，B 1，B 2，…，Bn为样本空间Ω的一个划分，且P（A）＞0，P（Bi）＞0（i＝1，2，…，n），则

式（1．3．4）称为贝叶斯（Bayes）公式．

证明　根据条件概率的定义、乘法公式和全概率公式，有

贝叶斯公式（1．3．4）的右边的分母是全概率公式（1．3．3）的右边，而分子则是全概率公式中相应的一项．

贝叶斯公式，由英国学者贝叶斯（Thomas Bayes）于1763年首次提出，在此基础上现在已经发展成“贝叶斯统计”，它在工程技术、经济管理、医学等领域都具有非常重要的实用价值．有兴趣的读者可参考《贝叶斯统计学及其应用》（韩明，2015）．

例1．3．5　3个电池生产车间甲、乙、丙，同时生产某种普通电池和某种高性能电池，1h的总产量为600只，各车间的产量见下表．

某1h因为出了差错没有在电池上加上车间的标签就放入了仓库．求：（1）在仓库里随机地取一只电池，它是高性能电池的概率是多少？（2）随机地取一只电池，已知它是高性能电池，它来自甲、乙、丙车间的概率各是多少？

解　设A表示“取到的是一只高性能电池”，B 1，B 2，B 3表示“取到的产品分别由甲、乙、丙车间生产的”．显然，B 1，B 2，B 3为样本空间Ω的一个划分，且有P（B 1）

（1）根据全概率公式

（2）根据贝叶斯公式

由于P（B 2|A）＞P（B 1|A）＞P（B 3|A），因此，这只电池来自乙车间的可能性最大．

例1．3．6　对以往数据分析结果表明，当机器调整得良好时，产品的合格率为0．98，而当机器发生某种故障时，其合格率为0．55．每天早上机器开动时，机器调整得良好的概率为0．95．试求已知某日早上第1件产品是合格品时机器调整得良好的概率．

解　设A表示“产品合格”，事件B表示“机器调整良好”，显然，B,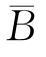为样本空间Ω的一个划分．根据题意，P（A|B）＝0．98，P（A|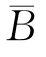）＝0．55，P（B）＝0．95，P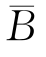（）＝0．05，所要求的概率为P（B|A）．根据贝叶斯公式，有

这个结果说明，当生产出第一件产品是合格品时机器调整得良好的概率为0．97．这里，概率0．95是由以往的数据分析得到的，叫做先验概率．而在得到信息（即生产出第一件产品是合格品）之后再重新加以修正的概率（即0．97）叫做后验概率．有了后验概率，我们就能对机器的情况有进一步的了解．