条件概率的乘法公式-概率论与数理统计（第5版）

在有些情况下，我们需要考虑事件A已经发生的条件下事件B发生的概率（记为P（B|A）），这种概率一般不同于P（B）．

例1．3．1　将一枚硬币抛掷2次，观察其出现正面（H）和反面（T）的情况．设事件A为“至少有1次出现正面（H）”，B为“2次掷出同一面”．现在来求事件A已经发生的条件下事件B发生的概率．

解　将一枚硬币抛掷2次，观察其出现正面（H）和反面（T）的情况，这个试验的样本空间为Ω＝｛HH，HT，TH，TT｝，且A＝｛HH，HT，TH｝，B＝｛HH，TT｝．易知，这是古典概型问题．

已知事件A已经发生，有了这个信息，知道了“TT”不能发生，即知试验所有可能结果所组成的集合就是A．A中有3个元素，其中只有HH∈B．于是，事件A已经发生的条件下事件B发生的概率为

在这里，我们看到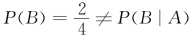．另外，易知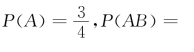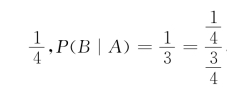，于是P（B|A）=

在例1．3．1中，有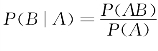． 在更一般的情况下，我们给出条件概率的定义．

定义1．3．1　设A，B是两个事件，且P（A）＞0，称

为在事件A发生的条件下事件B发生的条件概率．

不难验证，条件概率P（·|A）符合概率公理化定义中的3个公理，即

（1）非负性　对于每个事件B，有P（B|A）≥0；

（2）规范性　对于必然事件Ω，有P（Ω|A）＝1；

（3）可列可加性　若可列个事件B 1，B 2，…是两两互不相容的，则有

例1．3．2　设试验E为掷两颗骰子，观察出现的点数．用B表示事件“两颗骰子的点数相等”，用A表示事件“两颗骰子的点数之和为4”，求P（A|B），．(www.xing528.com)

解　以（i，j）表示第1颗骰子为i点，第2颗骰子为j点，则这个试验的样本空间为Ω＝｛（1，1），（1，2），…，（1，6），（2，1），（2，2），…，（2，6），…，（6，1），（6，2），…，（6，6）｝，且B＝｛（1，1），（2，2），（3，3），（4，4），（5，5），（6，6）｝，A＝｛（1，3），（2，2），（3，1）｝，AB＝｛（2，2）｝．

根据式（1．3．1），得

另外，也可以直接从条件概率的含义来考虑问题．当B发生时，样本空间缩减为Ω′＝B＝｛（1，1），（2，2），（3，3），（4，4），（5，5），（6，6）｝，在Ω′中只有样本点（2，2）∈A，于是,

同样，当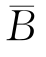发生时，样本空间缩减为Ω′′＝＝Ω-B，在Ω″中有30个样本点，其中只有样本点（1，3），（3，1）∈A，于是,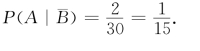

根据条件概率的定义，立即可以得到乘法公式．

定理1．3．1（乘法公式，或乘法定理）设P（A）＞0，则有

定理1．3．1可以推广到多个事件的情形．

设A 1，A 2，A 3是任意3个事件，且P（A 1A 2）＞0，则有

一般地，对于n个事件A 1，A 2，…，An（n≥2），且P（A 1A 2…An-1）＞0，则有

为什么这里仅要求“P（A 1A 2…An-1）＞0”？请读者思考．

例1．3．3　一个袋子中有7个白球和3个红球，从中不放回地取2个球，求第2次取到白球的概率．

解　设Ai＝“第i次取到白球”（i＝1，2），由于A 2＝A 1A 2∪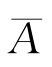 1A 2，且A 1A 2与 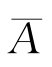1A 2互不相容，根据概率的有限可加性、乘法公式，有