【摘要】:我们继续考虑样本点的出现是等可能的随机试验,但不是古典概型那样局限于有限多个样本点的情形.将古典概型中的有限性推广到无限,而样本点的出现又有类似于古典概型中的等可能性,就得到几何概率.定义1.2.4(几何概率)如果试验E的样本点有无限多个,其样本空间Ω可用一个有度量的几何区域来表示,并且样本点落在Ω内任意一点处都是等可能的,其中A是Ω中的一个区域,样本点落在区域A的概率与A的测度(长度、面积、体积
我们继续考虑样本点的出现是等可能的随机试验,但不是古典概型那样局限于有限多个样本点的情形.将古典概型中的有限性推广到无限,而样本点的出现又有类似于古典概型中的等可能性,就得到几何概率.
定义1.2.4(几何概率)如果试验E的样本点有无限多个,其样本空间Ω可用一个有度量的几何区域来表示,并且样本点落在Ω内任意一点处都是等可能的,其中A是Ω中的一个区域,样本点落在区域A的概率与A的测度(长度、面积、体积等)成正比,而与A的位置和形状无关,则样本点落在区域A的概率为

式中,m(A)为区域A的测度,m(Ω)为区域Ω的测度,称上述概率为几何概率.
例1.2.5 在线段[0,3]上任意投一点,求此点的坐标小于1的概率.
解 当且仅当点落在[0,1)内时,此点的坐标小于1.根据几何概率的定义式
(1.2.2),所求的概率为(https://www.xing528.com)
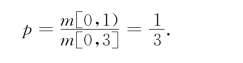
例1.2.6 (会面问题)两人相约在早晨8点到9点之间在某地会面,并约定先到者等候另一个人30min后就可以离开,求这两个人能见面的概率.
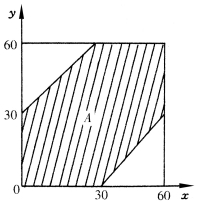
图1-8 会面问题
解 设8点x(min),8点y(min)分别表示两个人到达某地的时刻,由于两个人在8点到9点之间到达是随机的,因此,x,y都等可能地在[0,60]上取值,点(x,y)就是平面区域Ω={(x,y)|0≤x≤60,0≤y≤60}上等可能的随机点.设A=“两人能够会面”,根据题意,事件A发生的充分必要条件是|x-y|≤30,即随机点落在区域A={(x,y)||x-y|≤30}内,如图1-8所示.根据几何概率的定义式(1.2.2),所求的概率为
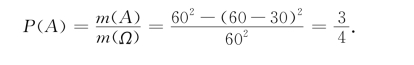
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




